Power Analysis and Simulation Tutorial
contributed by Lisa Schwetlick and Daniel Backhaus
This tutorial demonstrates how to conduct power analyses and data simulation using Julia and the MixedModelsSim package.
Power analysis is an important tool for planning an experimental design. Here we show how to:
- Use existing data as a basis for power calculations by simulating new data.
- Adapt parameters in a given linear mixed model to analyze power without changing the existing data set.
- Create a (simple) balanced fully crossed dataset from scratch and analyze power.
- Recreate a more complex dataset from scratch and analyze power for specific model parameter but various sample sizes.
Setup
Load the packages we'll be using in Julia
First, here are the packages needed in this example.
using MixedModels # run mixed models
using MixedModelsSim # simulation utilities
using DataFrames, Tables # work with dataframes
using StableRNGs # random number generator
using Statistics # basic statistical functions
using DataFrameMacros # dplyr-like operations
using CairoMakie # plotting package
CairoMakie.activate!(type="svg") # use vector graphics
using MixedModelsMakie # some extra plotting function for MixedModels
using ProgressMeter # show progress in loopsDefine number of iterations
Here we define how many model simulations we want to do. A large number will give more reliable results, but will take longer to compute. It is useful to set it to a low number for testing, and increase it for your final analysis.
# for real power analysis, set this much higher
nsims = 100100Use existing data to simulate new data
Build a linear mixed model from existing data
For the first example we are going to simulate data bootstrapped from an existing data set, namely Experiment 2 from
Kronmüller, E., & Barr, D. J. (2007). Perspective-free pragmatics: Broken precedents and the recovery-from-preemption hypothesis. Journal of Memory and Language, 56(3), 436-455.
This was an experiment about how in a conversation the change of a speaker or the change of precedents (which are patterns of word usage to describe an object, e.g. one can refer to the same object "white shoes", "runners", "sneakers") affects the understanding.
In experiment, objects were presented on a screen while participants listened to instructions to move the objects around. Participants' eye movements were tracked. The dependent variable is response time, defined as the latency between the onset of the test description and the moment at which the target was selected. The independent variables are speaker (old vs. new), precedents (maintain vs. break) and cognitive load (yes vs. no; from a secondary memory task).
We first load the data and define some characteristics like the contrasts and the underlying model. This dataset is one of the example datasets provided by MixedModels.jl.
Load existing data:
kb07 = MixedModels.dataset(:kb07);Arrow.Table with 1789 rows, 7 columns, and schema:
:subj String
:item String
:spkr String
:prec String
:load String
:rt_trunc Int16
:rt_raw Int16Set contrasts:
contrasts = Dict(:spkr => HelmertCoding(),
# set the reference level such that all the coefs
# have the same sign, which makes the plotting nicer
:prec => HelmertCoding(base="maintain"),
:load => HelmertCoding(),
# pseudo-contrast for grouping variables
:item => Grouping(),
:subj => Grouping());Dict{Symbol, StatsModels.AbstractContrasts} with 5 entries:
:item => Grouping()
:spkr => HelmertCoding(nothing, nothing)
:load => HelmertCoding(nothing, nothing)
:prec => HelmertCoding("maintain", nothing)
:subj => Grouping()The chosen linear mixed model (LMM) for this dataset is defined by the following model formula:
kb07_f = @formula(rt_trunc ~ 1 + spkr + prec + load + (1|subj) + (1 + prec|item));FormulaTerm
Response:
rt_trunc(unknown)
Predictors:
1
spkr(unknown)
prec(unknown)
load(unknown)
(subj)->1 | subj
(prec,item)->(1 + prec) | itemFit the model:
kb07_m = fit(MixedModel, kb07_f, kb07; contrasts=contrasts)Linear mixed model fit by maximum likelihood
rt_trunc ~ 1 + spkr + prec + load + (1 | subj) + (1 + prec | item)
logLik -2 logLik AIC AICc BIC
-14331.9251 28663.8501 28681.8501 28681.9513 28731.2548
Variance components:
Column Variance Std.Dev. Corr.
item (Intercept) 133015.244 364.713
prec: break 63766.937 252.521 +0.70
subj (Intercept) 88819.437 298.026
Residual 462443.388 680.032
Number of obs: 1789; levels of grouping factors: 32, 56
Fixed-effects parameters:
───────────────────────────────────────────────────
Coef. Std. Error z Pr(>|z|)
───────────────────────────────────────────────────
(Intercept) 2181.85 77.4681 28.16 <1e-99
spkr: old 67.879 16.0785 4.22 <1e-04
prec: break 333.791 47.4472 7.03 <1e-11
load: yes 78.5904 16.0785 4.89 <1e-05
───────────────────────────────────────────────────Simulate from existing data with same model parameters
We will first look at the power of the dataset with the same parameters as in the original data set. This means that each dataset will have the exact number of observations as the original data. Here, we use the model kb07_m we fitted above to our dataset kb07.
You can use the parametricbootstrap() function to run nsims iterations of data sampled using the parameters from kb07_m.
The parametric bootstrap is actually a simulation procedure. Each bootstrap iteration
- simulates new data based on an existing model
- then fits a model to that data to obtain new estimates.
Set up a random seed to make the simulation reproducible. You can use your favourite number.
To use multithreading, you need to set the number of worker threads you want to use. In VS Code, open the settings (gear icon in the lower left corner) and search for "thread". Set julia.NumThreads to the number of threads you want to use (at least 1 less than the total number of processor cores available, so that you can continue watching YouTube while the simulation runs).
Set random seed for reproducibility:
rng = StableRNG(42);StableRNGs.LehmerRNG(state=0x00000000000000000000000000000055)Run nsims iterations:
kb07_sim = parametricbootstrap(rng, nsims, kb07_m; use_threads = false);MixedModels.MixedModelBootstrap{Float64}(NamedTuple{(:objective, :σ, :β, :se, :θ), Tuple{Float64, Float64, NamedTuple{(Symbol("(Intercept)"), Symbol("spkr: old"), Symbol("prec: break"), Symbol("load: yes")), NTuple{4, Float64}}, StaticArrays.SVector{4, Float64}, StaticArrays.SVector{4, Float64}}}[(objective = 28621.661229666755, σ = 672.4984876136084, β = ((Intercept) = 2284.5565616513836, spkr: old = 29.059157857388694, prec: break = 379.9847240996829, load: yes = 53.200715604774025), se = [62.63963169345307, 15.900425247658747, 48.42912339528421, 15.900406020741057], θ = [0.39035223478357634, 0.0811060043510555, 0.3761437663643638, 0.43346299981295755]), (objective = 28700.426430502623, σ = 688.573917768676, β = ((Intercept) = 2123.4223232322893, spkr: old = 64.85037492579268, prec: break = 289.8956939282453, load: yes = 83.45915360894205), se = [86.34670283298404, 16.280453114285553, 56.52238497472776, 16.280432729535427], θ = [0.6432203885461479, 0.3570597714346811, 0.26502805641807237, 0.3539240890792213]), (objective = 28663.14607952808, σ = 682.3976258116478, β = ((Intercept) = 2107.3120184270847, spkr: old = 51.54052897959371, prec: break = 304.43149615775997, load: yes = 92.35230681682967), se = [72.002683946685, 16.134396757817633, 43.70289445752964, 16.13437407057551], θ = [0.4420781129827246, 0.283431979371174, 0.18173154065178948, 0.5001494374659511]), (objective = 28779.158761191586, σ = 707.0283499502617, β = ((Intercept) = 2057.3400310719258, spkr: old = 55.15524808115812, prec: break = 279.57450104821254, load: yes = 80.64505209526487), se = [71.03416501179495, 16.71679131755821, 44.69294723477344, 16.716770224071492], θ = [0.47910565325772836, 0.1968290393725666, 0.2668993514054729, 0.3636709953229884]), (objective = 28675.525825270495, σ = 689.3923893193219, β = ((Intercept) = 2197.1721220613595, spkr: old = 86.71558457858714, prec: break = 359.41313488286727, load: yes = 90.42962382327713), se = [68.7996970129149, 16.299780898888102, 39.98754812844367, 16.299759653040944], θ = [0.483399680572113, 0.20147940984306528, 0.22176630844084722, 0.34278026469355527]), (objective = 28657.229543391575, σ = 680.3764282029066, β = ((Intercept) = 2216.2801520043877, spkr: old = 72.6018160000202, prec: break = 295.3853472878758, load: yes = 78.84842558164799), se = [63.473196734017385, 16.086663472512427, 45.80467611086732, 16.08664361032543], θ = [0.3507396796989181, 0.2037699180390513, 0.2926146840744642, 0.4907089902862064]), (objective = 28613.203676274516, σ = 670.958543969336, β = ((Intercept) = 2188.6874261229946, spkr: old = 120.40236902161514, prec: break = 390.9056854910686, load: yes = 65.3828724833228), se = [77.14430833474337, 15.863979441107794, 48.26423456502853, 15.863958304091963], θ = [0.548776999389323, 0.2865396032789176, 0.2560991718965889, 0.42657421996152267]), (objective = 28612.538270903675, σ = 668.9735055375965, β = ((Intercept) = 2208.570880769515, spkr: old = 46.07531718827121, prec: break = 379.53461028854167, load: yes = 83.8064356660843), se = [77.5836994140038, 15.817029450986608, 47.563408656139934, 15.817007206373098], θ = [0.4884433660412176, 0.31848140253669766, 0.20601784213615493, 0.5517123246848117]), (objective = 28666.090916441728, σ = 682.3514738568468, β = ((Intercept) = 2048.335940184777, spkr: old = 101.35961649933571, prec: break = 264.15803942097625, load: yes = 66.83240557487974), se = [79.86379833636705, 16.133338916339188, 45.08488133246306, 16.133316826152797], θ = [0.5722596293372384, 0.2592694997653649, 0.23364549300022389, 0.40340737785658315]), (objective = 28656.104010757655, σ = 675.3422838611862, β = ((Intercept) = 2186.1183741584045, spkr: old = 76.67121242843318, prec: break = 398.8565855603288, load: yes = 104.5331407547283), se = [82.19813125503066, 15.967653309995141, 58.523364576651616, 15.967632813111273], θ = [0.583757484523986, 0.3487189164845196, 0.3175059151063801, 0.4493696202045406]) … (objective = 28659.658526619034, σ = 682.9637411905219, β = ((Intercept) = 2222.2437055753317, spkr: old = 73.02207002459515, prec: break = 396.61080497837975, load: yes = 59.786540898996975), se = [71.74673816968104, 16.14781209547503, 43.89562516697456, 16.147790979711356], θ = [0.5005975642159368, 0.23025039993042895, 0.24755904248923083, 0.38491618288111656]), (objective = 28728.441657129355, σ = 691.6685016337145, β = ((Intercept) = 2115.0960000560844, spkr: old = 83.38422399912129, prec: break = 289.15781518049846, load: yes = 62.148362842170165), se = [76.9571034455914, 16.353663479345094, 53.066338068086125, 16.353642934731905], θ = [0.5311794587923093, 0.24992230632772208, 0.3286509647000294, 0.4100956796516723]), (objective = 28645.8841424578, σ = 673.7034962399841, β = ((Intercept) = 2249.600213613422, spkr: old = 76.18822515771704, prec: break = 374.57458945155827, load: yes = 78.11102625264537), se = [82.32474112529856, 15.928897115857703, 46.42595846759869, 15.92887443147707], θ = [0.5483766958066294, 0.2735884221820423, 0.2433560463674676, 0.5278652240430557]), (objective = 28576.2730491512, σ = 662.553768633365, β = ((Intercept) = 2031.3129153946104, spkr: old = 48.41915971527457, prec: break = 227.56709416076018, load: yes = 72.316953003882), se = [77.13721334030691, 15.665276631412398, 41.970282814919706, 15.665254605308183], θ = [0.5334166243605396, 0.2153899908065603, 0.2532312666788933, 0.47939227839198895]), (objective = 28534.675383418853, σ = 653.3872313772034, β = ((Intercept) = 2158.5668830640434, spkr: old = 74.84688703289285, prec: break = 365.13366398206733, load: yes = 85.13975807208544), se = [73.37527972270632, 15.448563257943865, 50.872671784320545, 15.44854352063987], θ = [0.5192633391108868, 0.2395451391593742, 0.3445554809160844, 0.4506266534957814]), (objective = 28674.9434548781, σ = 679.9975467302435, β = ((Intercept) = 2133.610991054634, spkr: old = 65.02465694485448, prec: break = 380.8536874761602, load: yes = 88.108581341071), se = [83.9291997129054, 16.07770107780066, 46.25961054315295, 16.077677820217513], θ = [0.5642474163515199, 0.2817057947174507, 0.2254940496478204, 0.5144289761175916]), (objective = 28753.60390301111, σ = 696.6355510511909, β = ((Intercept) = 2123.5050082071825, spkr: old = 80.38728200773397, prec: break = 281.545521353235, load: yes = 59.4377611032154), se = [73.99969523817612, 16.471095390091758, 48.96909600620609, 16.47107368225166], θ = [0.4505185468048442, 0.2558404150776561, 0.2734508231715542, 0.49536375576123715]), (objective = 28738.06231225156, σ = 693.5002938567326, β = ((Intercept) = 2202.0914603208207, spkr: old = 83.60021148946889, prec: break = 356.44291323031666, load: yes = 106.50397759412284), se = [76.27512361801982, 16.396980894940715, 42.26085282927207, 16.39695834269736], θ = [0.4888827588732726, 0.15456921392488016, 0.2775812778131256, 0.47734402641685125]), (objective = 28623.208208054988, σ = 675.0618570896219, β = ((Intercept) = 2053.3096759861296, spkr: old = 38.37279478404601, prec: break = 264.6923118936408, load: yes = 127.72088232727523), se = [83.93050321658025, 15.960956597933283, 52.74487698383561, 15.960935514292421], θ = [0.6318387825967113, 0.3610502035131832, 0.21704484928734313, 0.3683825687219457]), (objective = 28669.41286642587, σ = 682.8361801711002, β = ((Intercept) = 2148.8346783160555, spkr: old = 66.23577574133499, prec: break = 353.28465311030607, load: yes = 71.429658632456), se = [74.21250033166844, 16.144820961290385, 44.94499006685252, 16.144800324734913], θ = [0.5259039834884985, 0.1829610510131432, 0.2954208475522838, 0.38230443325153846])], LinearAlgebra.LowerTriangular{Float64, Matrix{Float64}}[[0.5363168235433015 0.0; 0.25981993068702447 0.2653016008408132], [0.4382528209785196;;]], [[1, 2, 4], [1]], [0.0, -Inf, 0.0, 0.0], (item = ("(Intercept)", "prec: break"), subj = ("(Intercept)",)))Try: Run the code above with or without use_threads = true. Did performance get better or worse? Check out the help information parametricbootstrap to see why!
The returned value kb07_sim contains the results of the bootstrapping procedure, which we can convert to a dataframe
df = DataFrame(kb07_sim.allpars);
first(df, 12)12 rows × 5 columns
| iter | type | group | names | value | |
|---|---|---|---|---|---|
| Int64 | String | String? | String? | Float64 | |
| 1 | 1 | β | missing | (Intercept) | 2284.56 |
| 2 | 1 | β | missing | spkr: old | 29.0592 |
| 3 | 1 | β | missing | prec: break | 379.985 |
| 4 | 1 | β | missing | load: yes | 53.2007 |
| 5 | 1 | σ | item | (Intercept) | 262.511 |
| 6 | 1 | σ | item | prec: break | 258.77 |
| 7 | 1 | ρ | item | (Intercept), prec: break | 0.210781 |
| 8 | 1 | σ | subj | (Intercept) | 291.503 |
| 9 | 1 | σ | residual | missing | 672.498 |
| 10 | 2 | β | missing | (Intercept) | 2123.42 |
| 11 | 2 | β | missing | spkr: old | 64.8504 |
| 12 | 2 | β | missing | prec: break | 289.896 |
The dataframe df has 4500 rows: 9 parameters, each from 500 iterations.
nrow(df)900We can now plot some bootstrapped parameters:
fig = Figure()
σres = @subset(df, :type == "σ" && :group == "residual")
ax = Axis(fig[1,1:2]; xlabel = "residual standard deviation", ylabel = "Density")
density!(ax, σres.value)
βInt = @subset(df, :type == "β" && :names == "(Intercept)")
ax = Axis(fig[1,3]; xlabel = "fixed effect for intercept")
density!(ax, βInt.value)
βSpeaker = @subset(df, :type == "β" && :names == "spkr: old")
ax = Axis(fig[2,1]; xlabel = "fixed effect for spkr: old", ylabel = "Density")
density!(ax, βSpeaker.value)
βPrecedents = @subset(df, :type == "β" && :names == "prec: break")
ax = Axis(fig[2,2]; xlabel = "fixed effect for prec: break")
density!(ax, βPrecedents.value)
βLoad = @subset(df, :type == "β" && :names == "load: yes")
ax = Axis(fig[2,3]; xlabel = "fixed effect for load: yes")
density!(ax, βLoad.value)
Label(fig[0,:]; text = "Parametric bootstrap replicates by parameter", textsize=25)
figFor the fixed effects, we can do this more succinctly via the ridgeplot functionality in MixedModelsMakie, even optionally omitting the intercept (which we often don't care about).
ridgeplot(kb07_sim; show_intercept=false)Next, we extract the p-values of the fixed-effects parameters into a dataframe
kb07_sim_df = DataFrame(kb07_sim.coefpvalues);
first(kb07_sim_df, 8)8 rows × 6 columns
| iter | coefname | β | se | z | p | |
|---|---|---|---|---|---|---|
| Int64 | Symbol | Float64 | Float64 | Float64 | Float64 | |
| 1 | 1 | (Intercept) | 2284.56 | 62.6396 | 36.4714 | 3.14813e-291 |
| 2 | 1 | spkr: old | 29.0592 | 15.9004 | 1.82757 | 0.0676139 |
| 3 | 1 | prec: break | 379.985 | 48.4291 | 7.8462 | 4.28823e-15 |
| 4 | 1 | load: yes | 53.2007 | 15.9004 | 3.34587 | 0.000820244 |
| 5 | 2 | (Intercept) | 2123.42 | 86.3467 | 24.5918 | 1.54532e-133 |
| 6 | 2 | spkr: old | 64.8504 | 16.2805 | 3.98333 | 6.7957e-5 |
| 7 | 2 | prec: break | 289.896 | 56.5224 | 5.12887 | 2.91494e-7 |
| 8 | 2 | load: yes | 83.4592 | 16.2804 | 5.12635 | 2.95417e-7 |
Now that we have a bootstrapped data, we can start our power calculation.
Power calculation
The function power_table() from MixedModelsSim takes the output of parametricbootstrap() and calculates the proportion of simulations where the p-value is less than alpha for each coefficient. You can set the alpha argument to change the default value of 0.05 (justify your alpha).
ptbl = power_table(kb07_sim, 0.05)4-element Vector{NamedTuple{(:coefname, :power), Tuple{String, Float64}}}:
(coefname = "prec: break", power = 1.0)
(coefname = "(Intercept)", power = 1.0)
(coefname = "spkr: old", power = 0.99)
(coefname = "load: yes", power = 1.0)An estimated power of 1 means that in every iteration the specific parameter we are looking at was below our alpha. An estimated power of 0.5 means that in half of our iterations the specific parameter we are looking at was below our alpha. An estimated power of 0 means that for none of our iterations the specific parameter we are looking at was below our alpha.
You can also do it manually:
prec_p = kb07_sim_df[kb07_sim_df.coefname .== Symbol("prec: break"),:p]
mean(prec_p .< 0.05)1.0For a nicer display, you can use pretty_table:
pretty_table(ptbl)┌─────────────┬─────────┐
│ coefname │ power │
│ String │ Float64 │
├─────────────┼─────────┤
│ prec: break │ 1.0 │
│ (Intercept) │ 1.0 │
│ spkr: old │ 0.99 │
│ load: yes │ 1.0 │
└─────────────┴─────────┘The simulation so far should not be interpreted as the power of the original K&B experiment. Observed power calculations are generally problematic. Instead, the example so far should serve to show how power can be computed using a simulation procedure.
In the next section, we show how to use previously observed data – such as pilot data – as the basis for a simulation study with a different effect size.
Adapt parameters in a given linear mixed model to analyze power without generating additional data
Let's say we want to check our power to detect effects of spkr, prec, and load that are only half the size as in our pilot data. We can set a new vector of beta values (fixed effects) with the β argument to parametricbootstrap().
Specify β:
new_beta = kb07_m.β
new_beta[2:4] = kb07_m.β[2:4] / 23-element Vector{Float64}:
33.939510821752606
166.89531060681816
39.29522053308301Run simulations:
kb07_sim_half = parametricbootstrap(StableRNG(42), nsims, kb07_m; β = new_beta, use_threads = false);MixedModels.MixedModelBootstrap{Float64}(NamedTuple{(:objective, :σ, :β, :se, :θ), Tuple{Float64, Float64, NamedTuple{(Symbol("(Intercept)"), Symbol("spkr: old"), Symbol("prec: break"), Symbol("load: yes")), NTuple{4, Float64}}, StaticArrays.SVector{4, Float64}, StaticArrays.SVector{4, Float64}}}[(objective = 28621.661229666748, σ = 672.4984876067797, β = ((Intercept) = 2284.5565616509725, spkr: old = -4.880352964761857, prec: break = 213.08941349325895, load: yes = 13.905495072113172), se = [62.6396315257178, 15.900425247497171, 48.429123675828144, 15.900406020579528], θ = [0.3903522328925455, 0.08110600677962201, 0.3761437684009502, 0.4334629998030897]), (objective = 28700.426430502615, σ = 688.5739178635357, β = ((Intercept) = 2123.422323232717, spkr: old = 30.91086410477843, prec: break = 123.00038332069731, load: yes = 44.16393307544727), se = [86.34670190588143, 16.280453116529475, 56.52238453159425, 16.280432731779428], θ = [0.6432203804205713, 0.35705976406061946, 0.26502805986230554, 0.3539240878646748]), (objective = 28663.14607952807, σ = 682.3976256077425, β = ((Intercept) = 2107.312018426256, spkr: old = 17.60101815798097, prec: break = 137.53618555081047, load: yes = 53.05708628457647), se = [72.0026843880668, 16.134396752997677, 43.70289466991051, 16.134374065755523], θ = [0.44207811644498046, 0.283431981473413, 0.1817315410985943, 0.5001494401244329]), (objective = 28779.15876119159, σ = 707.0283499985873, β = ((Intercept) = 2057.3400310717457, spkr: old = 21.215737259175313, prec: break = 112.67919044162805, load: yes = 41.34983156237415), se = [71.03416494448895, 16.716791318700494, 44.69294710280936, 16.716770225213754], θ = [0.4791056525862864, 0.1968290385074115, 0.2668993505961831, 0.36367099529199803]), (objective = 28675.52582527049, σ = 689.3923893126041, β = ((Intercept) = 2197.1721220606946, spkr: old = 52.77607375647418, prec: break = 192.5178242764119, load: yes = 51.13440329086487), se = [68.79969680346385, 16.299780898729747, 39.98754818050651, 16.299759652882617], θ = [0.48339967837400416, 0.20147940959376698, 0.22176630930415103, 0.3427802651806746]), (objective = 28657.229543391575, σ = 680.3764282416495, β = ((Intercept) = 2216.2801520044973, spkr: old = 38.662305178343736, prec: break = 128.49003668098447, load: yes = 39.55320504845572), se = [63.473196626242576, 16.08666347342841, 45.80467604845868, 16.08664361124143], θ = [0.350739678434053, 0.2037699166990331, 0.29261468430407656, 0.4907089901253385]), (objective = 28613.203676274516, σ = 670.9585439665078, β = ((Intercept) = 2188.687426123016, spkr: old = 86.46285819985293, prec: break = 224.01037488425916, load: yes = 26.087651950228114), se = [77.14430830180623, 15.863979441041012, 48.26423456294649, 15.863958304025184], θ = [0.5487769990107889, 0.28653960310812365, 0.2560991720625186, 0.4265742200800853]), (objective = 28612.538270903693, σ = 668.973505189292, β = ((Intercept) = 2208.5708807710125, spkr: old = 12.135806367258114, prec: break = 212.63929968097847, load: yes = 44.51121513148973), se = [77.58370001085227, 15.817029442755114, 47.56340905830487, 15.81700719814163], θ = [0.4884433716573019, 0.3184814045012072, 0.2060178461470546, 0.5517123271970082]), (objective = 28666.09091644174, σ = 682.35147385448, β = ((Intercept) = 2048.335940184646, spkr: old = 67.420105677423, prec: break = 97.26272881431521, load: yes = 27.5371850419161), se = [79.86379826811894, 16.133338916283467, 45.08488129602509, 16.13331682609708], θ = [0.5722596286430248, 0.25926949901747526, 0.23364549334896806, 0.403407377961497]), (objective = 28656.104010757677, σ = 675.3422836638351, β = ((Intercept) = 2186.1183741587697, spkr: old = 42.731701606978014, prec: break = 231.96127495319672, load: yes = 65.23792022125485), se = [82.19813165467964, 15.967653305330257, 58.52336478395938, 15.967632808446371], θ = [0.5837574878186812, 0.3487189175082646, 0.31750591688414925, 0.4493696222298901]) … (objective = 28659.65852661943, σ = 682.9637460793749, β = ((Intercept) = 2222.243705601032, spkr: old = 39.082559251894054, prec: break = 229.71549432251075, load: yes = 20.491320340210798), se = [71.74673413266505, 16.147812211016387, 43.89561830730528, 16.147791095251595], θ = [0.5005975337150739, 0.23025038835238257, 0.24755896599066513, 0.3849161504644015]), (objective = 28728.441657129344, σ = 691.6685016266435, β = ((Intercept) = 2115.0960000561277, spkr: old = 49.44471317735593, prec: break = 122.26250457370308, load: yes = 22.85314230907547), se = [76.95710347934114, 16.353663479177946, 53.06633804134403, 16.353642934564753], θ = [0.5311794590547628, 0.24992230618499273, 0.3286509645256017, 0.41009567981539247]), (objective = 28645.884142457795, σ = 673.7034962379792, β = ((Intercept) = 2249.600213612855, spkr: old = 42.248714335650384, prec: break = 207.67927884505582, load: yes = 38.81580572011459), se = [82.32474087914574, 15.928897115810843, 46.42595815089379, 15.928874431430188], θ = [0.5483766919681935, 0.27358841822188995, 0.243356046561682, 0.5278652262895006]), (objective = 28576.273049006002, σ = 662.5539420812698, β = ((Intercept) = 2031.312918064458, spkr: old = 14.479648523813882, prec: break = 60.67178392365831, load: yes = 33.02172980099407), se = [77.13671331423765, 15.66528072957842, 41.97164118791718, 15.665258703702548], θ = [0.5334137502192584, 0.21540779135436655, 0.2532324046427612, 0.4793871965858932]), (objective = 28534.675383418842, σ = 653.3872311601319, β = ((Intercept) = 2158.56688306463, spkr: old = 40.90737621073501, prec: break = 198.23835337565106, load: yes = 45.84453753841039), se = [73.37528009386997, 15.448563252812576, 50.872671944071115, 15.448543515508542], θ = [0.5192633413972447, 0.2395451409503964, 0.3445554816259319, 0.45062665733355384]), (objective = 28674.943454878117, σ = 679.9975467023585, β = ((Intercept) = 2133.610991054915, spkr: old = 31.085146123628853, prec: break = 213.95837686879239, load: yes = 48.81336080764531), se = [83.9291997005921, 16.077701077142162, 46.2596104995641, 16.07767781955903], θ = [0.5642474164380936, 0.28170579330971257, 0.2254940508145759, 0.5144289757761409]), (objective = 28753.603903011102, σ = 696.6355511711779, β = ((Intercept) = 2123.5050082068688, spkr: old = 46.44777118560962, prec: break = 114.6502107467901, load: yes = 20.14254057045031), se = [73.99969510918231, 16.471095392928046, 48.96909580284351, 16.471073685087934], θ = [0.450518546397861, 0.2558404135662281, 0.2734508220847187, 0.4953637539657039]), (objective = 28738.062312251684, σ = 693.5002936082077, β = ((Intercept) = 2202.0914603217057, spkr: old = 49.66070066742297, prec: break = 189.54760262379224, load: yes = 67.2087570601525), se = [76.27512461785389, 16.396980889064398, 42.260853054156954, 16.396958336820948], θ = [0.48888276788851753, 0.1545692228155621, 0.27758127529388593, 0.47734402937001125]), (objective = 28623.20820805498, σ = 675.0618570672322, β = ((Intercept) = 2053.3096759859463, spkr: old = 4.433283962082526, prec: break = 97.79700128703281, load: yes = 88.42566179437459), se = [83.9305032841685, 15.960956597403923, 52.74487695553777, 15.960935513763035], θ = [0.6318387830206154, 0.3610502035173642, 0.21704484882735353, 0.368382569419834]), (objective = 28669.412866425857, σ = 682.836180140093, β = ((Intercept) = 2148.83467831612, spkr: old = 32.29626491964494, prec: break = 186.38934250342584, load: yes = 32.134438099317634), se = [74.21250042472303, 16.144820960557446, 44.94499006697151, 16.144800324001963], θ = [0.5259039843096892, 0.1829610509820431, 0.29542084759409526, 0.3823044335227172])], LinearAlgebra.LowerTriangular{Float64, Matrix{Float64}}[[0.5363168235433015 0.0; 0.25981993068702447 0.2653016008408132], [0.4382528209785196;;]], [[1, 2, 4], [1]], [0.0, -Inf, 0.0, 0.0], (item = ("(Intercept)", "prec: break"), subj = ("(Intercept)",)))Power calculation
power_table(kb07_sim_half)4-element Vector{NamedTuple{(:coefname, :power), Tuple{String, Float64}}}:
(coefname = "prec: break", power = 0.93)
(coefname = "(Intercept)", power = 1.0)
(coefname = "spkr: old", power = 0.54)
(coefname = "load: yes", power = 0.73)Create and analyze a (simple) balanced fully crossed dataset from scratch
In some situations, instead of using an existing dataset it may be useful to simulate the data from scratch. This could be the case when pilot data or data from a previous study are not available. Note that we still have to assume (or perhaps guess) a particular effect size, which can be derived from previous work (whether experimental or practical). In the worst case, we can start from the smallest effect size that we would find interesting or meaningful.
In order to simulate data from scratch, we have to:
- specify the effect sizes manually
- manually create an experimental design, according to which data can be simulated
If we simulate data from scratch, we can manipulate the arguments β, σ and θ (in addition to the number of subjects and items) Lets have a closer look at them, define their meaning and we will see where the corresponding values in the model output are.
Fixed Effects (βs)
β are our effect sizes.
If we look again on our LMM summary from the kb07-dataset kb07_m we see our four β under fixed-effects parameters in the Coef.-column.
kb07_mLinear mixed model fit by maximum likelihood
rt_trunc ~ 1 + spkr + prec + load + (1 | subj) + (1 + prec | item)
logLik -2 logLik AIC AICc BIC
-14331.9251 28663.8501 28681.8501 28681.9513 28731.2548
Variance components:
Column Variance Std.Dev. Corr.
item (Intercept) 133015.244 364.713
prec: break 63766.937 252.521 +0.70
subj (Intercept) 88819.437 298.026
Residual 462443.388 680.032
Number of obs: 1789; levels of grouping factors: 32, 56
Fixed-effects parameters:
───────────────────────────────────────────────────
Coef. Std. Error z Pr(>|z|)
───────────────────────────────────────────────────
(Intercept) 2181.85 77.4681 28.16 <1e-99
spkr: old 67.879 16.0785 4.22 <1e-04
prec: break 333.791 47.4472 7.03 <1e-11
load: yes 78.5904 16.0785 4.89 <1e-05
───────────────────────────────────────────────────kb07_m.β4-element Vector{Float64}:
2181.852639290988
67.87902164350521
333.7906212136363
78.59044106616602(These can also be accessed with the appropriately named coef function.)
Residual Variance (σ)
σ is the residual-standard deviation listed under the variance components.
kb07_m.σ680.0319022257572Random Effects (θ)
The meaning of θ is a bit less intuitive. In a less complex model (one that only has intercepts for the random effects) or if we suppress the correlations in the formula with zerocorr() then θ describes the relationship between the standard deviation of the random effects and the residual standard deviation.
In our kb07_m example:
- The
residualstandard deviation is680.032. - The standard deviation of our first variance component
item (Intercept)is364.713. - Thus our first
θis the relationship: variance component devided byresidualstandard deviation: $364.713 / 680.032 = 0.53631$
kb07_m.θ4-element Vector{Float64}:
0.5363168235433015
0.25981993068702447
0.2653016008408132
0.4382528209785196We also can calculate the θ for variance component subj (Intercept). The residual standard deviation is 680.032. The standard deviation of our variance component subj (Intercept) is 298.026. Thus, the related θ is the relationship: variance component devided by residual standard deviation 298.026 / 680.032 = 0.438252
We can not calculate the θs for variance component item prec: break this way, because it includes the correlation of item prec: break and item (Intercept). But keep in mind that the relation of item prec: break-variability (252.521) and the residual-variability (680.032) is $252.521 / 680.032 = 0.3713369$.
The θ vector is the flattened version of the lower Cholesky factor variance-covariance matrix. The Cholesky factor is in some sense a "matrix square root" (so like storing standard deviations instead of variances) and is a lower triangular matrix. The on-diagonal elements are just the standard deviations (the σ's). If all off-diagonal elements are zero, we can use our calculation above. The off-diagonal elements are covariances and correspond to the correlations (the ρ's). If they are unequal to zero, as it is in our kb07-dataset, one way to get the two missing θ-values is to take the values directly from the model we have already fitted.
See the two inner values:
kb07_m.θ4-element Vector{Float64}:
0.5363168235433015
0.25981993068702447
0.2653016008408132
0.4382528209785196Another way is to make use of the create_re() function. Here you have to define the relation of all random effects variabilities to the variability of the residuals, as shown above, and the correlation-matrices.
Let's start by defining the correlation matrix for the item-part.
The diagonal is always 1.0 because everything is perfectly correlated with itself. The elements below the diagonal follow the same form as the Corr. entries in the output of VarCorr(). In our example the correlation of item prec: break and item (Intercept) is -0.7. The elements above the diagonal are just a mirror image.
re_item_corr = [1.0 -0.7; -0.7 1.0]2×2 Matrix{Float64}:
1.0 -0.7
-0.7 1.0Now we put together all relations of standard deviations and the correlation-matrix for the item-group. This calculates the covariance factorization which is the theta matrix.
re_item = create_re(0.536, 0.371; corrmat = re_item_corr)2×2 LinearAlgebra.LowerTriangular{Float64, Matrix{Float64}}:
0.536 ⋅
-0.2597 0.264947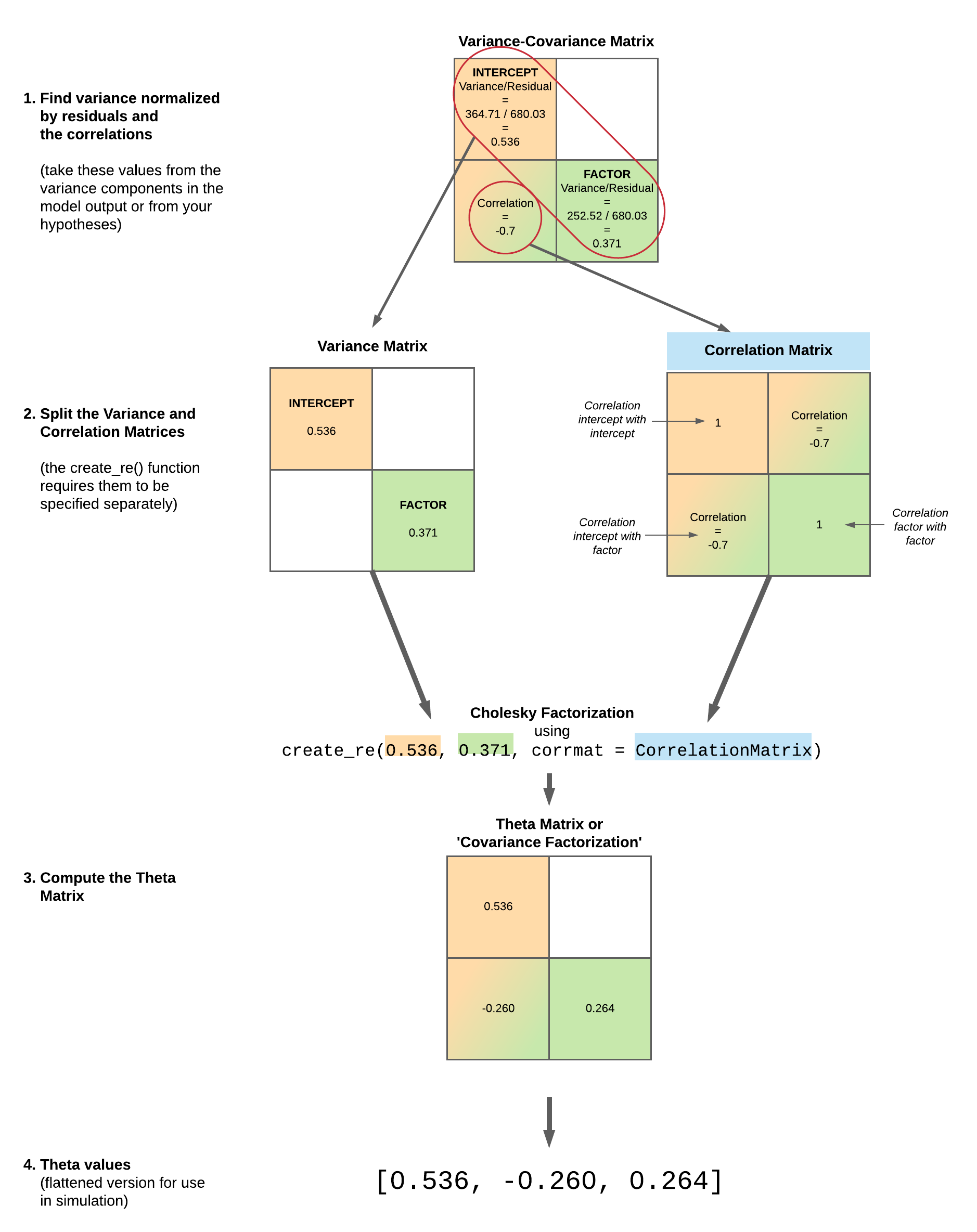
Don't be too specific with your values in create_re(). Generally we don't these values very precisely because estimating them precisely requires large amounts of data. Additionally, if there are numerical problems (rounding errors), you will get the error-message: PosDefException: matrix is not Hermitian; Cholesky factorization failed.
Although we advise against using these values, you can extract the exact values like so (just as a pedagogical demonstration):
corr_exact = VarCorr(kb07_m).σρ.item.ρ[1]
σ_residuals_exact = kb07_m.σ
σ_1_exact = VarCorr(kb07_m).σρ.item.σ[1] / σ_residuals_exact
σ_2_exact = VarCorr(kb07_m).σρ.item.σ[2] / σ_residuals_exact
re_item_corr = [1.0 corr_exact; corr_exact 1.0]
re_item = create_re(σ_1_exact, σ_2_exact; corrmat = re_item_corr)2×2 LinearAlgebra.LowerTriangular{Float64, Matrix{Float64}}:
0.536317 ⋅
0.25982 0.265302Let's continue with the subj-part.
Since there the by-subject random effects have only one entry (the intercept), there are no correlations to specify and we can omit the corrmat argument.
Now we put together all relations of standard deviations and the correlation-matrix for the subj-group:
This calculates the covariance factorization which is the theta matrix.
re_subj = create_re(0.438)1×1 LinearAlgebra.LowerTriangular{Float64, LinearAlgebra.Diagonal{Float64, Vector{Float64}}}:
0.438If you want the exact value you can use
σ_residuals_exact = kb07_m.σ
σ_3_exact = VarCorr(kb07_m).σρ.subj.σ[1] / σ_residuals_exact
re_subj = create_re(σ_3_exact)1×1 LinearAlgebra.LowerTriangular{Float64, LinearAlgebra.Diagonal{Float64, Vector{Float64}}}:
0.43825282097851964As mentioned above θ is the compact form of these covariance matrices:
createθ(kb07_m; item=re_item, subj=re_subj)4-element Vector{Float64}:
0.5363168235433015
0.2598199306870244
0.2653016008408133
0.43825282097851964The function createθ is putting the random effects into the correct order and then putting them into the compact form. Even for the same formula, the order may vary between datasets (and hence models fit to those datasets) because of a particular computational trick used in MixedModels.jl. Because of this trick, we need to specify the model along with the random effects so that the correct order can be determined.
We can install these parameter in the parametricbootstrap()-function or in the model like this:
# need the fully qualified name here because Makie also defines update!
MixedModelsSim.update!(kb07_m, item=re_item, subj=re_subj)Linear mixed model fit by maximum likelihood
rt_trunc ~ 1 + spkr + prec + load + (1 | subj) + (1 + prec | item)
logLik -2 logLik AIC AICc BIC
-14331.9251 28663.8501 28681.8501 28681.9513 28731.2548
Variance components:
Column Variance Std.Dev. Corr.
item (Intercept) 133015.244 364.713
prec: break 63766.937 252.521 +0.70
subj (Intercept) 88819.437 298.026
Residual 462443.388 680.032
Number of obs: 1789; levels of grouping factors: 32, 56
Fixed-effects parameters:
───────────────────────────────────────────────────
Coef. Std. Error z Pr(>|z|)
───────────────────────────────────────────────────
(Intercept) 2181.85 77.4681 28.16 <1e-99
spkr: old 67.879 16.0785 4.22 <1e-04
prec: break 333.791 47.4472 7.03 <1e-11
load: yes 78.5904 16.0785 4.89 <1e-05
───────────────────────────────────────────────────A simple example from scratch
Having this knowledge about the parameters we can now simulate data from scratch
The simdat_crossed() function from MixedModelsSim lets you set up a data frame with a specified experimental design. For now, it only makes fully balanced crossed designs, but you can generate an unbalanced design by simulating data for the largest cell and deleting extra rows.
First, we will set an easy design where subj_n subjects per age group (Old or Young) respond to item_n items in each of two conditions (A or B).
Your factors need to be specified separately for between-subject, between-item, and within-subject/item factors using Dict with the name of each factor as the keys and vectors with the names of the levels as values.
We start with the between subject factors:
subj_btwn = Dict(:age => ["O", "Y"])Dict{Symbol, Vector{String}} with 1 entry:
:age => ["O", "Y"]There are no between-item factors in this design so you can omit it or set it to nothing. Note that if you have factors which are between subject and between item, you need to put them in both dicts.
item_btwn = nothingNext, we put within-subject/item factors in a dict:
both_win = Dict(:condition => ["A", "B"])Dict{Symbol, Vector{String}} with 1 entry:
:condition => ["A", "B"]Define subject and item number:
subj_n = 10
item_n = 3030Simulate data:
dat = simdat_crossed(subj_n,
item_n,
subj_btwn = subj_btwn,
item_btwn = item_btwn,
both_win = both_win);600-element Vector{NamedTuple{(:subj, :age, :item, :condition, :dv), Tuple{String, String, String, String, Float64}}}:
(subj = "S01", age = "O", item = "I01", condition = "A", dv = 0.3695620056052401)
(subj = "S02", age = "Y", item = "I01", condition = "A", dv = -1.7781166660111283)
(subj = "S03", age = "O", item = "I01", condition = "A", dv = 0.0011829274912199899)
(subj = "S04", age = "Y", item = "I01", condition = "A", dv = -1.4232750494451083)
(subj = "S05", age = "O", item = "I01", condition = "A", dv = 1.013459219994095)
(subj = "S06", age = "Y", item = "I01", condition = "A", dv = 1.0073491488577841)
(subj = "S07", age = "O", item = "I01", condition = "A", dv = 1.4761576287561835)
(subj = "S08", age = "Y", item = "I01", condition = "A", dv = -0.7076910739843743)
(subj = "S09", age = "O", item = "I01", condition = "A", dv = -0.33240711038735427)
(subj = "S10", age = "Y", item = "I01", condition = "A", dv = -0.038819668669192994)
⋮
(subj = "S02", age = "Y", item = "I30", condition = "B", dv = 0.3347804482550522)
(subj = "S03", age = "O", item = "I30", condition = "B", dv = -0.05449140625693583)
(subj = "S04", age = "Y", item = "I30", condition = "B", dv = -0.264934295754025)
(subj = "S05", age = "O", item = "I30", condition = "B", dv = 0.6057246237925421)
(subj = "S06", age = "Y", item = "I30", condition = "B", dv = 0.7581515422231916)
(subj = "S07", age = "O", item = "I30", condition = "B", dv = -0.7695175043041778)
(subj = "S08", age = "Y", item = "I30", condition = "B", dv = 0.1750326080013378)
(subj = "S09", age = "O", item = "I30", condition = "B", dv = -0.4785843539356276)
(subj = "S10", age = "Y", item = "I30", condition = "B", dv = 0.30611969702901)Have a look:
first(DataFrame(dat),8)8 rows × 5 columns
| subj | age | item | condition | dv | |
|---|---|---|---|---|---|
| String | String | String | String | Float64 | |
| 1 | S01 | O | I01 | A | 0.369562 |
| 2 | S02 | Y | I01 | A | -1.77812 |
| 3 | S03 | O | I01 | A | 0.00118293 |
| 4 | S04 | Y | I01 | A | -1.42328 |
| 5 | S05 | O | I01 | A | 1.01346 |
| 6 | S06 | Y | I01 | A | 1.00735 |
| 7 | S07 | O | I01 | A | 1.47616 |
| 8 | S08 | Y | I01 | A | -0.707691 |
The values we see in the column dv is just random noise (drawn from the standard normal distribution)
Set contrasts:
contrasts = Dict(:age => HelmertCoding(),
:condition => HelmertCoding(),
:subj => Grouping(),
:item => Grouping());Dict{Symbol, StatsModels.AbstractContrasts} with 4 entries:
:item => Grouping()
:age => HelmertCoding(nothing, nothing)
:condition => HelmertCoding(nothing, nothing)
:subj => Grouping()Define formula:
f1 = @formula(dv ~ 1 + age * condition + (1|item) + (1|subj));FormulaTerm
Response:
dv(unknown)
Predictors:
1
age(unknown)
condition(unknown)
(item)->1 | item
(subj)->1 | subj
age(unknown) & condition(unknown)Note that we did not include condition as random slopes for item and subject. This is mainly to keep the example simple and to keep the parameter θ easier to understand (see Section 3 above for the explanation of θ).
Fit the model:
m1 = fit(MixedModel, f1, dat; contrasts=contrasts)Linear mixed model fit by maximum likelihood
dv ~ 1 + age + condition + age & condition + (1 | item) + (1 | subj)
logLik -2 logLik AIC AICc BIC
-850.6655 1701.3310 1715.3310 1715.5202 1746.1096
Variance components:
Column Variance Std.Dev.
item (Intercept) 0.000000 0.000000
subj (Intercept) 0.000000 0.000000
Residual 0.997677 0.998838
Number of obs: 600; levels of grouping factors: 30, 10
Fixed-effects parameters:
──────────────────────────────────────────────────────────────
Coef. Std. Error z Pr(>|z|)
──────────────────────────────────────────────────────────────
(Intercept) -0.050657 0.0407774 -1.24 0.2141
age: Y -0.0386301 0.0407774 -0.95 0.3435
condition: B 0.0407199 0.0407774 1.00 0.3180
age: Y & condition: B -0.0825374 0.0407774 -2.02 0.0430
──────────────────────────────────────────────────────────────Because the dv is just random noise from N(0,1), there will be basically no subject or item random variance, residual variance will be near 1.0, and the estimates for all effects should be small. Don't worry, we'll specify fixed and random effects directly in parametricbootstrap().
Set random seed for reproducibility:
rng = StableRNG(42);StableRNGs.LehmerRNG(state=0x00000000000000000000000000000055)Specify β, σ, and θ, we just made up this parameter:
new_beta = [0., 0.25, 0.25, 0.]
new_sigma = 2.0
new_theta = [1.0, 1.0]2-element Vector{Float64}:
1.0
1.0Run nsims iterations:
sim1 = parametricbootstrap(rng, nsims, m1;
β = new_beta,
σ = new_sigma,
θ = new_theta,
use_threads = false);MixedModels.MixedModelBootstrap{Float64}(NamedTuple{(:objective, :σ, :β, :se, :θ), Tuple{Float64, Float64, NamedTuple{(Symbol("(Intercept)"), Symbol("age: Y"), Symbol("condition: B"), Symbol("age: Y & condition: B")), NTuple{4, Float64}}, StaticArrays.SVector{4, Float64}, StaticArrays.SVector{2, Float64}}}[(objective = 2692.3610314326565, σ = 2.0478784220880417, β = ((Intercept) = -1.2514691972111587, age: Y = 1.0092232885828807, condition: B = 0.2234187328428466, age: Y & condition: B = 0.06947075238301066), se = [0.720793039536988, 0.6118632760171087, 0.08360428648952764, 0.08360428648952764], θ = [1.019034338389846, 0.9359609240930048]), (objective = 2637.687645491678, σ = 1.9664599289732207, β = ((Intercept) = 0.593330407689209, age: Y = 0.16250401624005328, condition: B = 0.06184620640928383, age: Y & condition: B = -0.12242391752570914), se = [0.7344968193080423, 0.663752949102254, 0.08028039042690069, 0.08028039042690069], θ = [0.8760165516149474, 1.0595496560478799]), (objective = 2584.144014882135, σ = 1.88053534333703, β = ((Intercept) = 0.12032043743901674, age: Y = 0.16126672420500401, condition: B = 0.27531489351217514, age: Y & condition: B = 0.06880234926264961), se = [0.512030787949158, 0.3559679552274456, 0.07677253390742163, 0.07677253390742163], θ = [1.0719842836952442, 0.5845025519086687]), (objective = 2674.0451340881073, σ = 2.0068020172637477, β = ((Intercept) = -0.08942325214774097, age: Y = 1.2445124382240942, condition: B = 0.2756056156168278, age: Y & condition: B = 0.001931994712891143), se = [0.8064188854808368, 0.7041897654315777, 0.08192734928473568, 0.08192734928473568], θ = [1.072554559578576, 1.102112383726077]), (objective = 2687.7463371553745, σ = 2.0633485113327543, β = ((Intercept) = -0.6692467458281229, age: Y = 0.5105132739560936, condition: B = 0.20596770138857237, age: Y & condition: B = -0.02567416416820537), se = [0.5568391657485752, 0.4433791063792454, 0.08423585023827537, 0.08423585023827537], θ = [0.8942458505635478, 0.6671443587404873]), (objective = 2676.45595836345, σ = 2.0373920161845227, β = ((Intercept) = 0.4394355388817665, age: Y = 0.17931804380054658, condition: B = 0.3439411667123485, age: Y & condition: B = 0.11467757327199374), se = [0.7436384906091953, 0.6778629981170785, 0.08317618076120546, 0.08317618076120546], θ = [0.8220377106432257, 1.044174452656469]), (objective = 2662.5516127573765, σ = 2.0073631998040935, β = ((Intercept) = -0.5461799640539833, age: Y = -0.020800285880993065, condition: B = 0.32158228755740875, age: Y & condition: B = -0.06355472394332844), se = [0.5695549460776099, 0.42531462506959544, 0.08195025946600912, 0.08195025946600912], θ = [1.033620426402125, 0.6574595717511161]), (objective = 2636.7044040219616, σ = 1.9547764909528393, β = ((Intercept) = -0.3166835135942215, age: Y = 0.4757914674418319, condition: B = 0.32305158582986443, age: Y & condition: B = 0.07193706539215138), se = [0.7909222263262863, 0.7141321535896172, 0.07980341606704457, 0.07980341606704457], θ = [0.952559593853057, 1.1480286223578147]), (objective = 2690.427621457432, σ = 2.0452657137815247, β = ((Intercept) = 0.5834695426913963, age: Y = -0.08265650422636776, condition: B = 0.22652487157529644, age: Y & condition: B = -0.08648642349416014), se = [0.7132932075712201, 0.6040754002415482, 0.083497623119566, 0.083497623119566], θ = [1.0158071633800136, 0.925022909471881]), (objective = 2708.548257715347, σ = 2.0835992733126862, β = ((Intercept) = 0.3589849794878493, age: Y = -0.15549678679448367, condition: B = 0.23911665978067326, age: Y & condition: B = 0.0006507184175729405), se = [0.6930264849504829, 0.5897517514868975, 0.08506258413416515, 0.08506258413416515], θ = [0.9567958060985956, 0.885706729305045]) … (objective = 2637.953771647583, σ = 1.9842597758457563, β = ((Intercept) = 0.5624601448509483, age: Y = 2.035284607902874, condition: B = 0.27385209102044317, age: Y & condition: B = -0.023771509877653734), se = [0.6520863508073856, 0.5920857475403949, 0.08100706613252381, 0.08100706613252381], θ = [0.7541888996504788, 0.9347227889309166]), (objective = 2658.694677765881, σ = 2.007900160343729, β = ((Intercept) = 0.5605369038496382, age: Y = 0.9185091186664979, condition: B = 0.20189088196302704, age: Y & condition: B = -0.02141332492747582), se = [0.5626614691241847, 0.44306537846580557, 0.08197218078824439, 0.08197218078824439], θ = [0.9460563969791229, 0.6857451194850108]), (objective = 2676.0209006214213, σ = 2.0083185965629275, β = ((Intercept) = 0.9187827821596537, age: Y = -0.7412780384350917, condition: B = 0.15986383394434417, age: Y & condition: B = -0.012568512706629953), se = [0.6741813238985664, 0.5019648849767719, 0.08198926337535999, 0.08198926337535999], θ = [1.2274278595807802, 0.7797740980446296]), (objective = 2636.285217088517, σ = 1.981537927306236, β = ((Intercept) = 0.5180933838121901, age: Y = -0.02380164095586062, condition: B = 0.29354273633215955, age: Y & condition: B = 0.08734688663859327), se = [0.5669093139971536, 0.48535770972149217, 0.08089594713120773, 0.08089594713120773], θ = [0.8097248593959852, 0.7637335262606444]), (objective = 2661.361754846196, σ = 1.9970235459424313, β = ((Intercept) = -0.12923626375649858, age: Y = 0.34126300340694926, condition: B = 0.29045825647582413, age: Y & condition: B = 0.09646631934185002), se = [0.617296217103909, 0.4730812445198234, 0.08152814486470794, 0.08152814486470794], θ = [1.087604637522747, 0.737914011160372]), (objective = 2737.151617178374, σ = 2.1149977572155394, β = ((Intercept) = 0.2759725559383551, age: Y = 0.12611603784254008, condition: B = 0.30420567292028156, age: Y & condition: B = 0.03363570717209671), se = [0.7647988593650162, 0.6254988613048856, 0.08634442187181485, 0.08634442187181485], θ = [1.139672782785549, 0.9262727278274115]), (objective = 2662.0588866146113, σ = 1.9838399912145264, β = ((Intercept) = -0.10945975366426486, age: Y = 0.8786858809755225, condition: B = 0.1578602858946256, age: Y & condition: B = 0.09809830059469302), se = [0.7862677398214485, 0.6733672727547533, 0.08098992849671754, 0.08098992849671754], θ = [1.1207893411192884, 1.0655678282043348]), (objective = 2654.167217165058, σ = 2.0101301800305476, β = ((Intercept) = -0.48939838916341105, age: Y = 0.37511524023648346, condition: B = 0.17421380067393283, age: Y & condition: B = -0.01750520590571173), se = [0.5558292086695502, 0.46294204173784587, 0.08206322096072884, 0.08206322096072884], θ = [0.8382096224895011, 0.7167530931156135]), (objective = 2746.499890360901, σ = 2.1201823571552287, β = ((Intercept) = 0.20097785295453707, age: Y = -0.4535819594043264, condition: B = 0.338843517460014, age: Y & condition: B = -0.02264787332360139), se = [0.8168065584581601, 0.6562382761859051, 0.08655608227802657, 0.08655608227802657], θ = [1.2563923245301944, 0.9702360443903194]), (objective = 2660.5285117476787, σ = 2.000112356724207, β = ((Intercept) = 0.3251552146834756, age: Y = 1.004221072897235, condition: B = 0.18809918940694131, age: Y & condition: B = 0.011991756750343306), se = [0.8925027412317148, 0.8370180858100864, 0.08165424503683058, 0.08165424503683058], θ = [0.8483119388550033, 1.3170553318859473])], LinearAlgebra.LowerTriangular{Float64, Matrix{Float64}}[[0.0;;], [0.0;;]], [[1], [1]], [0.0, 0.0], (item = ("(Intercept)",), subj = ("(Intercept)",)))Power calculation
ptbl= power_table(sim1)4-element Vector{NamedTuple{(:coefname, :power), Tuple{String, Float64}}}:
(coefname = "age: Y", power = 0.23)
(coefname = "condition: B", power = 0.86)
(coefname = "(Intercept)", power = 0.08)
(coefname = "age: Y & condition: B", power = 0.04)For nicely displaying it, you can use pretty_table:
pretty_table(ptbl)┌───────────────────────┬─────────┐
│ coefname │ power │
│ String │ Float64 │
├───────────────────────┼─────────┤
│ age: Y │ 0.23 │
│ condition: B │ 0.86 │
│ (Intercept) │ 0.08 │
│ age: Y & condition: B │ 0.04 │
└───────────────────────┴─────────┘Compute power curves for a more complex dataset
Recreate the kb07-dataset from scratch
For full control over all parameters in our kb07 data set we will recreate the design using the method shown above.
Define subject and item number:
subj_n = 56
item_n = 3232Define factors in a dict:
subj_btwn = nothing
item_btwn = nothing
both_win = Dict(:spkr => ["old", "new"],
:prec => ["maintain", "break"],
:load => ["yes", "no"]);Dict{Symbol, Vector{String}} with 3 entries:
:spkr => ["old", "new"]
:load => ["yes", "no"]
:prec => ["maintain", "break"]Try: Play with simdat_crossed.
Simulate data:
fake_kb07 = simdat_crossed(subj_n, item_n,
subj_btwn = subj_btwn,
item_btwn = item_btwn,
both_win = both_win);14336-element Vector{NamedTuple{(:subj, :item, :spkr, :load, :prec, :dv), Tuple{String, String, String, String, String, Float64}}}:
(subj = "S01", item = "I01", spkr = "old", load = "yes", prec = "maintain", dv = 0.27057099454894346)
(subj = "S02", item = "I01", spkr = "old", load = "yes", prec = "maintain", dv = 0.3892838376374773)
(subj = "S03", item = "I01", spkr = "old", load = "yes", prec = "maintain", dv = 0.8300111927389338)
(subj = "S04", item = "I01", spkr = "old", load = "yes", prec = "maintain", dv = -0.955496590999253)
(subj = "S05", item = "I01", spkr = "old", load = "yes", prec = "maintain", dv = 0.192525887508059)
(subj = "S06", item = "I01", spkr = "old", load = "yes", prec = "maintain", dv = -1.030363172450139)
(subj = "S07", item = "I01", spkr = "old", load = "yes", prec = "maintain", dv = -0.553405829510012)
(subj = "S08", item = "I01", spkr = "old", load = "yes", prec = "maintain", dv = 2.8846125070311697)
(subj = "S09", item = "I01", spkr = "old", load = "yes", prec = "maintain", dv = 0.14031395027343835)
(subj = "S10", item = "I01", spkr = "old", load = "yes", prec = "maintain", dv = -0.32364818606189616)
⋮
(subj = "S48", item = "I32", spkr = "new", load = "no", prec = "break", dv = 0.04229756916761708)
(subj = "S49", item = "I32", spkr = "new", load = "no", prec = "break", dv = 1.3911110908846909)
(subj = "S50", item = "I32", spkr = "new", load = "no", prec = "break", dv = 1.5491490991900847)
(subj = "S51", item = "I32", spkr = "new", load = "no", prec = "break", dv = -0.45425770775509744)
(subj = "S52", item = "I32", spkr = "new", load = "no", prec = "break", dv = 0.5481605364729785)
(subj = "S53", item = "I32", spkr = "new", load = "no", prec = "break", dv = 0.28871718679074765)
(subj = "S54", item = "I32", spkr = "new", load = "no", prec = "break", dv = 1.6922570964860095)
(subj = "S55", item = "I32", spkr = "new", load = "no", prec = "break", dv = -0.1321259464985056)
(subj = "S56", item = "I32", spkr = "new", load = "no", prec = "break", dv = -0.6948893688767375)Make a dataframe:
fake_kb07_df = DataFrame(fake_kb07);Have a look:
first(fake_kb07_df,8)8 rows × 6 columns
| subj | item | spkr | load | prec | dv | |
|---|---|---|---|---|---|---|
| String | String | String | String | String | Float64 | |
| 1 | S01 | I01 | old | yes | maintain | 0.270571 |
| 2 | S02 | I01 | old | yes | maintain | 0.389284 |
| 3 | S03 | I01 | old | yes | maintain | 0.830011 |
| 4 | S04 | I01 | old | yes | maintain | -0.955497 |
| 5 | S05 | I01 | old | yes | maintain | 0.192526 |
| 6 | S06 | I01 | old | yes | maintain | -1.03036 |
| 7 | S07 | I01 | old | yes | maintain | -0.553406 |
| 8 | S08 | I01 | old | yes | maintain | 2.88461 |
The function simdat_crossed generates a balanced fully crossed design. Unfortunately, our original design is not balanced fully crossed. Every subject saw an image only once, thus in one of eight possible conditions. To simulate that we only keep one of every eight lines.
We sort the dataframe to enable easier selection
sort!(fake_kb07_df, [:subj, :item, :load, :prec, :spkr])In order to select only the relevant rows of the data set we define an index which represents a random choice of one of every eight rows. First we generate a vector idx which represents which row to keep in each set of 8.
len = div(length(fake_kb07), 8) # integer division
idx = rand(rng, 1:8 , len)
show(idx)[8, 7, 7, 6, 1, 8, 7, 3, 1, 6, 4, 6, 2, 3, 5, 8, 3, 1, 2, 7, 2, 2, 3, 2, 5, 7, 3, 6, 1, 6, 2, 6, 6, 2, 6, 3, 3, 7, 6, 3, 1, 1, 6, 2, 4, 6, 3, 4, 8, 3, 5, 5, 5, 6, 4, 6, 8, 6, 8, 6, 6, 7, 3, 1, 2, 4, 4, 2, 7, 2, 3, 4, 2, 7, 5, 8, 3, 6, 4, 3, 6, 1, 5, 8, 4, 7, 5, 1, 8, 4, 7, 4, 2, 4, 6, 7, 2, 3, 2, 6, 8, 1, 4, 6, 8, 8, 5, 7, 2, 2, 2, 6, 8, 8, 2, 8, 5, 1, 3, 1, 3, 7, 3, 1, 7, 6, 5, 1, 1, 4, 3, 3, 8, 2, 7, 1, 6, 6, 3, 5, 7, 3, 2, 3, 6, 5, 2, 8, 5, 1, 4, 4, 2, 8, 6, 1, 7, 8, 7, 2, 4, 8, 5, 8, 4, 7, 7, 2, 4, 8, 7, 1, 2, 5, 4, 4, 5, 3, 7, 6, 4, 6, 8, 7, 7, 5, 6, 1, 1, 6, 2, 3, 1, 4, 4, 7, 1, 2, 1, 6, 7, 2, 5, 3, 2, 4, 6, 4, 4, 1, 5, 4, 2, 4, 3, 7, 4, 7, 4, 1, 3, 2, 4, 1, 6, 4, 1, 3, 1, 8, 8, 5, 4, 4, 3, 3, 6, 6, 5, 5, 7, 8, 7, 8, 1, 2, 4, 3, 3, 5, 6, 7, 6, 8, 1, 6, 2, 1, 3, 7, 1, 6, 1, 5, 7, 3, 8, 5, 1, 2, 6, 3, 1, 8, 4, 6, 7, 7, 3, 3, 5, 4, 7, 2, 7, 8, 2, 3, 3, 8, 7, 8, 6, 3, 8, 5, 5, 2, 5, 3, 1, 2, 6, 2, 4, 8, 8, 8, 1, 1, 4, 1, 2, 6, 1, 7, 3, 3, 5, 1, 6, 3, 2, 5, 5, 5, 4, 3, 6, 1, 2, 7, 1, 5, 2, 2, 5, 1, 3, 8, 4, 3, 1, 5, 1, 7, 5, 2, 5, 5, 5, 2, 6, 5, 5, 8, 2, 4, 5, 7, 8, 3, 7, 2, 3, 5, 1, 6, 3, 8, 4, 8, 8, 2, 6, 6, 7, 2, 7, 7, 3, 2, 8, 1, 5, 4, 4, 3, 4, 1, 5, 2, 6, 2, 7, 8, 7, 3, 3, 4, 3, 4, 2, 3, 8, 5, 8, 1, 2, 3, 1, 2, 3, 6, 2, 5, 1, 2, 4, 8, 6, 6, 3, 1, 5, 6, 2, 1, 3, 4, 7, 4, 6, 4, 5, 4, 3, 6, 6, 3, 4, 7, 2, 8, 8, 5, 4, 1, 5, 6, 4, 7, 5, 1, 8, 2, 2, 7, 4, 3, 7, 5, 2, 7, 1, 3, 7, 1, 2, 6, 1, 1, 2, 5, 4, 5, 8, 3, 3, 3, 6, 4, 6, 5, 4, 4, 8, 1, 5, 8, 4, 6, 1, 4, 4, 7, 3, 8, 4, 8, 6, 2, 3, 4, 2, 7, 2, 4, 3, 7, 6, 2, 7, 5, 2, 7, 4, 3, 3, 2, 8, 3, 2, 3, 2, 7, 5, 8, 6, 4, 3, 1, 8, 7, 8, 3, 7, 6, 2, 5, 4, 6, 6, 1, 8, 8, 4, 3, 6, 2, 6, 6, 4, 3, 6, 1, 5, 4, 2, 2, 1, 3, 5, 6, 5, 8, 7, 2, 6, 6, 7, 1, 5, 3, 7, 3, 8, 8, 1, 7, 4, 8, 3, 6, 6, 1, 4, 3, 7, 8, 4, 3, 5, 2, 3, 8, 7, 6, 6, 6, 4, 7, 3, 7, 2, 1, 7, 2, 4, 7, 1, 1, 2, 8, 1, 6, 4, 6, 6, 2, 5, 3, 5, 8, 6, 6, 3, 6, 7, 7, 5, 8, 3, 6, 6, 8, 8, 6, 1, 6, 8, 7, 7, 7, 6, 6, 3, 5, 4, 7, 2, 2, 6, 2, 1, 6, 8, 1, 6, 7, 7, 7, 7, 1, 1, 1, 4, 4, 3, 1, 2, 8, 7, 3, 3, 6, 5, 2, 7, 3, 6, 4, 2, 6, 5, 4, 8, 5, 3, 2, 6, 7, 8, 6, 5, 8, 1, 1, 7, 4, 1, 4, 4, 1, 6, 1, 2, 1, 2, 8, 2, 7, 5, 4, 5, 2, 6, 7, 7, 2, 7, 6, 3, 6, 6, 6, 4, 5, 1, 7, 1, 7, 3, 4, 5, 6, 3, 1, 5, 3, 2, 3, 8, 7, 3, 3, 3, 4, 4, 8, 2, 1, 6, 2, 4, 5, 4, 6, 2, 1, 7, 8, 1, 5, 4, 6, 1, 3, 7, 8, 8, 5, 8, 7, 1, 1, 7, 2, 7, 8, 8, 4, 1, 4, 8, 3, 5, 2, 3, 4, 1, 6, 6, 2, 2, 5, 5, 2, 2, 8, 2, 3, 7, 1, 5, 7, 6, 3, 1, 6, 6, 6, 3, 7, 5, 7, 7, 7, 4, 8, 1, 1, 6, 2, 8, 4, 6, 2, 3, 6, 8, 4, 7, 7, 3, 2, 3, 3, 7, 3, 7, 4, 7, 5, 5, 1, 6, 4, 6, 3, 6, 1, 7, 3, 7, 5, 7, 6, 4, 4, 6, 7, 2, 2, 4, 5, 6, 7, 8, 4, 5, 3, 5, 3, 8, 2, 6, 6, 7, 3, 8, 8, 6, 6, 6, 4, 8, 2, 5, 4, 4, 3, 4, 4, 7, 6, 6, 5, 7, 4, 8, 4, 4, 6, 8, 5, 7, 6, 3, 2, 3, 7, 1, 1, 3, 3, 3, 4, 7, 8, 7, 2, 5, 1, 6, 7, 3, 1, 5, 2, 4, 5, 5, 1, 5, 7, 4, 4, 7, 5, 6, 8, 6, 3, 5, 3, 8, 3, 4, 8, 5, 6, 2, 2, 2, 6, 2, 7, 2, 4, 7, 8, 6, 7, 8, 3, 4, 6, 3, 2, 2, 6, 2, 4, 6, 7, 2, 8, 7, 2, 8, 5, 3, 6, 3, 7, 5, 4, 3, 1, 6, 6, 7, 6, 3, 5, 3, 2, 6, 4, 4, 1, 7, 7, 5, 5, 5, 7, 4, 6, 1, 2, 7, 7, 8, 4, 4, 1, 1, 5, 3, 5, 3, 7, 8, 5, 6, 7, 2, 3, 1, 5, 4, 1, 4, 7, 2, 6, 8, 1, 3, 7, 3, 1, 8, 7, 7, 4, 7, 4, 1, 7, 5, 7, 1, 1, 2, 4, 4, 1, 8, 3, 5, 2, 7, 5, 2, 5, 6, 8, 5, 5, 7, 1, 3, 8, 1, 1, 2, 4, 7, 6, 4, 8, 5, 4, 5, 6, 3, 3, 7, 8, 8, 6, 6, 2, 4, 7, 5, 6, 8, 2, 2, 4, 7, 2, 7, 6, 8, 7, 2, 8, 4, 2, 6, 6, 4, 3, 5, 7, 8, 1, 5, 7, 5, 6, 7, 4, 1, 3, 4, 7, 3, 7, 1, 6, 6, 2, 4, 1, 1, 5, 5, 5, 4, 6, 8, 6, 2, 2, 6, 3, 5, 7, 6, 4, 6, 4, 8, 8, 7, 1, 4, 2, 6, 5, 2, 6, 7, 5, 7, 5, 3, 2, 1, 6, 6, 1, 6, 5, 6, 6, 8, 5, 3, 3, 4, 2, 3, 6, 2, 7, 1, 6, 2, 3, 3, 8, 8, 7, 5, 4, 8, 5, 5, 7, 7, 4, 8, 5, 2, 5, 7, 3, 8, 5, 7, 1, 5, 3, 5, 7, 6, 6, 6, 1, 2, 7, 3, 6, 2, 2, 3, 5, 3, 8, 8, 6, 4, 6, 6, 5, 3, 1, 8, 8, 6, 1, 6, 7, 1, 8, 6, 2, 7, 6, 8, 4, 2, 4, 4, 8, 1, 2, 3, 7, 5, 1, 3, 4, 7, 8, 6, 7, 4, 6, 5, 3, 6, 6, 1, 2, 7, 4, 2, 6, 6, 5, 5, 3, 3, 7, 3, 6, 8, 4, 7, 5, 3, 5, 8, 6, 3, 3, 3, 1, 7, 6, 2, 2, 4, 8, 3, 5, 8, 8, 3, 7, 4, 4, 7, 8, 4, 5, 5, 2, 7, 8, 7, 4, 6, 5, 7, 6, 7, 7, 2, 2, 7, 7, 5, 2, 6, 8, 4, 8, 6, 1, 8, 1, 7, 8, 2, 7, 7, 5, 6, 7, 4, 2, 3, 6, 4, 7, 8, 8, 6, 1, 5, 6, 5, 5, 8, 2, 6, 5, 6, 1, 4, 1, 8, 6, 7, 2, 5, 3, 2, 3, 6, 6, 2, 4, 7, 8, 7, 1, 3, 7, 8, 2, 2, 3, 4, 4, 6, 1, 1, 6, 3, 7, 4, 6, 8, 2, 4, 6, 3, 2, 2, 8, 1, 6, 7, 3, 1, 5, 3, 7, 6, 7, 2, 7, 4, 3, 8, 4, 6, 1, 4, 1, 2, 6, 1, 7, 5, 4, 6, 7, 3, 7, 3, 5, 7, 2, 7, 4, 7, 1, 8, 1, 5, 1, 3, 3, 8, 6, 1, 7, 8, 3, 4, 4, 3, 3, 2, 7, 5, 3, 6, 1, 1, 6, 2, 1, 5, 7, 2, 7, 2, 5, 1, 6, 4, 8, 4, 2, 8, 2, 1, 4, 8, 8, 3, 3, 2, 3, 3, 5, 1, 3, 7, 4, 2, 7, 5, 8, 3, 5, 2, 4, 6, 5, 5, 5, 1, 2, 4, 7, 1, 4, 2, 6, 8, 5, 4, 4, 4, 1, 1, 5, 6, 3, 7, 2, 2, 4, 4, 6, 4, 2, 2, 4, 8, 4, 2, 8, 4, 2, 4, 4, 4, 5, 2, 1, 1, 7, 6, 8, 7, 6, 3, 1, 2, 1, 2, 2, 5, 3, 5, 4, 6, 4, 6, 2, 3, 4, 8, 7, 8, 6, 1, 8, 1, 4, 1, 4, 5, 2, 3, 2, 2, 6, 7, 4, 8, 7, 8, 5, 7, 7, 8, 2, 2, 4, 5, 2, 8, 8, 5, 8, 7, 7, 1, 2, 6, 4, 6, 2, 6, 1, 2, 6, 2, 7, 1, 3, 2, 4, 2, 5, 7, 4, 5, 6, 6, 7, 4, 6, 8, 5, 2, 3, 8, 8, 7, 8, 2, 4, 7, 5, 1, 7, 7, 1, 5, 8, 8, 4, 5, 4, 6, 4, 8, 7, 2, 3, 5, 6, 5, 2, 6, 7, 2, 2, 4, 8, 6, 5, 7, 3, 8, 1, 2, 6, 3, 7, 3, 2, 2, 3, 2, 7, 8, 5, 8, 4, 4, 7, 6, 5, 6, 7, 5, 5, 4, 3, 4, 3, 5, 7, 8, 3, 5, 3, 3, 5, 5, 4, 4, 1, 6, 5, 1, 6, 3, 2, 5, 2, 8, 3, 5, 1, 5, 2, 6, 2, 3, 3, 8, 5, 6, 7, 3, 2, 2, 4, 1, 7, 8, 6, 8, 2, 5, 8, 3, 8, 2, 8, 8, 1, 2, 1, 1, 7, 2, 2, 3, 8, 4, 7, 6, 6, 5, 8, 6, 5, 5, 7, 6, 7, 2, 1]Then we create an array A, of the same length that is populated multiples of the number 8. Added together A and idx give the indexes of one row from each set of 8s.
A = repeat([8], inner=len-1)
push!(A, 0)
A = cumsum(A)
idx = idx .+ A
show(idx)[16, 23, 31, 38, 41, 56, 63, 67, 73, 86, 92, 102, 106, 115, 125, 136, 139, 145, 154, 167, 170, 178, 187, 194, 205, 215, 219, 230, 233, 246, 250, 262, 270, 274, 286, 291, 299, 311, 318, 323, 329, 337, 350, 354, 364, 374, 379, 388, 400, 403, 413, 421, 429, 438, 444, 454, 464, 470, 480, 486, 494, 503, 507, 513, 522, 532, 540, 546, 559, 562, 571, 580, 586, 599, 605, 616, 619, 630, 636, 643, 654, 657, 669, 680, 684, 695, 701, 705, 720, 724, 735, 740, 746, 756, 766, 775, 778, 787, 794, 806, 816, 817, 828, 838, 848, 856, 861, 871, 874, 882, 890, 902, 912, 920, 922, 936, 941, 945, 955, 961, 971, 983, 987, 993, 1007, 1014, 1021, 1025, 1033, 1044, 1051, 1059, 1072, 1074, 1087, 1089, 1102, 1110, 1115, 1125, 1135, 1139, 1146, 1155, 1166, 1173, 1178, 1192, 1197, 1201, 1212, 1220, 1226, 1240, 1246, 1249, 1263, 1272, 1279, 1282, 1292, 1304, 1309, 1320, 1324, 1335, 1343, 1346, 1356, 1368, 1375, 1377, 1386, 1397, 1404, 1412, 1421, 1427, 1439, 1446, 1452, 1462, 1472, 1479, 1487, 1493, 1502, 1505, 1513, 1526, 1530, 1539, 1545, 1556, 1564, 1575, 1577, 1586, 1593, 1606, 1615, 1618, 1629, 1635, 1642, 1652, 1662, 1668, 1676, 1681, 1693, 1700, 1706, 1716, 1723, 1735, 1740, 1751, 1756, 1761, 1771, 1778, 1788, 1793, 1806, 1812, 1817, 1827, 1833, 1848, 1856, 1861, 1868, 1876, 1883, 1891, 1902, 1910, 1917, 1925, 1935, 1944, 1951, 1960, 1961, 1970, 1980, 1987, 1995, 2005, 2014, 2023, 2030, 2040, 2041, 2054, 2058, 2065, 2075, 2087, 2089, 2102, 2105, 2117, 2127, 2131, 2144, 2149, 2153, 2162, 2174, 2179, 2185, 2200, 2204, 2214, 2223, 2231, 2235, 2243, 2253, 2260, 2271, 2274, 2287, 2296, 2298, 2307, 2315, 2328, 2335, 2344, 2350, 2355, 2368, 2373, 2381, 2386, 2397, 2403, 2409, 2418, 2430, 2434, 2444, 2456, 2464, 2472, 2473, 2481, 2492, 2497, 2506, 2518, 2521, 2535, 2539, 2547, 2557, 2561, 2574, 2579, 2586, 2597, 2605, 2613, 2620, 2627, 2638, 2641, 2650, 2663, 2665, 2677, 2682, 2690, 2701, 2705, 2715, 2728, 2732, 2739, 2745, 2757, 2761, 2775, 2781, 2786, 2797, 2805, 2813, 2818, 2830, 2837, 2845, 2856, 2858, 2868, 2877, 2887, 2896, 2899, 2911, 2914, 2923, 2933, 2937, 2950, 2955, 2968, 2972, 2984, 2992, 2994, 3006, 3014, 3023, 3026, 3039, 3047, 3051, 3058, 3072, 3073, 3085, 3092, 3100, 3107, 3116, 3121, 3133, 3138, 3150, 3154, 3167, 3176, 3183, 3187, 3195, 3204, 3211, 3220, 3226, 3235, 3248, 3253, 3264, 3265, 3274, 3283, 3289, 3298, 3307, 3318, 3322, 3333, 3337, 3346, 3356, 3368, 3374, 3382, 3387, 3393, 3405, 3414, 3418, 3425, 3435, 3444, 3455, 3460, 3470, 3476, 3485, 3492, 3499, 3510, 3518, 3523, 3532, 3543, 3546, 3560, 3568, 3573, 3580, 3585, 3597, 3606, 3612, 3623, 3629, 3633, 3648, 3650, 3658, 3671, 3676, 3683, 3695, 3701, 3706, 3719, 3721, 3731, 3743, 3745, 3754, 3766, 3769, 3777, 3786, 3797, 3804, 3813, 3824, 3827, 3835, 3843, 3854, 3860, 3870, 3877, 3884, 3892, 3904, 3905, 3917, 3928, 3932, 3942, 3945, 3956, 3964, 3975, 3979, 3992, 3996, 4008, 4014, 4018, 4027, 4036, 4042, 4055, 4058, 4068, 4075, 4087, 4094, 4098, 4111, 4117, 4122, 4135, 4140, 4147, 4155, 4162, 4176, 4179, 4186, 4195, 4202, 4215, 4221, 4232, 4238, 4244, 4251, 4257, 4272, 4279, 4288, 4291, 4303, 4310, 4314, 4325, 4332, 4342, 4350, 4353, 4368, 4376, 4380, 4387, 4398, 4402, 4414, 4422, 4428, 4435, 4446, 4449, 4461, 4468, 4474, 4482, 4489, 4499, 4509, 4518, 4525, 4536, 4543, 4546, 4558, 4566, 4575, 4577, 4589, 4595, 4607, 4611, 4624, 4632, 4633, 4647, 4652, 4664, 4667, 4678, 4686, 4689, 4700, 4707, 4719, 4728, 4732, 4739, 4749, 4754, 4763, 4776, 4783, 4790, 4798, 4806, 4812, 4823, 4827, 4839, 4842, 4849, 4863, 4866, 4876, 4887, 4889, 4897, 4906, 4920, 4921, 4934, 4940, 4950, 4958, 4962, 4973, 4979, 4989, 5000, 5006, 5014, 5019, 5030, 5039, 5047, 5053, 5064, 5067, 5078, 5086, 5096, 5104, 5110, 5113, 5126, 5136, 5143, 5151, 5159, 5166, 5174, 5179, 5189, 5196, 5207, 5210, 5218, 5230, 5234, 5241, 5254, 5264, 5265, 5278, 5287, 5295, 5303, 5311, 5313, 5321, 5329, 5340, 5348, 5355, 5361, 5370, 5384, 5391, 5395, 5403, 5414, 5421, 5426, 5439, 5443, 5454, 5460, 5466, 5478, 5485, 5492, 5504, 5509, 5515, 5522, 5534, 5543, 5552, 5558, 5565, 5576, 5577, 5585, 5599, 5604, 5609, 5620, 5628, 5633, 5646, 5649, 5658, 5665, 5674, 5688, 5690, 5703, 5709, 5716, 5725, 5730, 5742, 5751, 5759, 5762, 5775, 5782, 5787, 5798, 5806, 5814, 5820, 5829, 5833, 5847, 5849, 5863, 5867, 5876, 5885, 5894, 5899, 5905, 5917, 5923, 5930, 5939, 5952, 5959, 5963, 5971, 5979, 5988, 5996, 6008, 6010, 6017, 6030, 6034, 6044, 6053, 6060, 6070, 6074, 6081, 6095, 6104, 6105, 6117, 6124, 6134, 6137, 6147, 6159, 6168, 6176, 6181, 6192, 6199, 6201, 6209, 6223, 6226, 6239, 6248, 6256, 6260, 6265, 6276, 6288, 6291, 6301, 6306, 6315, 6324, 6329, 6342, 6350, 6354, 6362, 6373, 6381, 6386, 6394, 6408, 6410, 6419, 6431, 6433, 6445, 6455, 6462, 6467, 6473, 6486, 6494, 6502, 6507, 6519, 6525, 6535, 6543, 6551, 6556, 6568, 6569, 6577, 6590, 6594, 6608, 6612, 6622, 6626, 6635, 6646, 6656, 6660, 6671, 6679, 6683, 6690, 6699, 6707, 6719, 6723, 6735, 6740, 6751, 6757, 6765, 6769, 6782, 6788, 6798, 6803, 6814, 6817, 6831, 6835, 6847, 6853, 6863, 6870, 6876, 6884, 6894, 6903, 6906, 6914, 6924, 6933, 6942, 6951, 6960, 6964, 6973, 6979, 6989, 6995, 7008, 7010, 7022, 7030, 7039, 7043, 7056, 7064, 7070, 7078, 7086, 7092, 7104, 7106, 7117, 7124, 7132, 7139, 7148, 7156, 7167, 7174, 7182, 7189, 7199, 7204, 7216, 7220, 7228, 7238, 7248, 7253, 7263, 7270, 7275, 7282, 7291, 7303, 7305, 7313, 7323, 7331, 7339, 7348, 7359, 7368, 7375, 7378, 7389, 7393, 7406, 7415, 7419, 7425, 7437, 7442, 7452, 7461, 7469, 7473, 7485, 7495, 7500, 7508, 7519, 7525, 7534, 7544, 7550, 7555, 7565, 7571, 7584, 7587, 7596, 7608, 7613, 7622, 7626, 7634, 7642, 7654, 7658, 7671, 7674, 7684, 7695, 7704, 7710, 7719, 7728, 7731, 7740, 7750, 7755, 7762, 7770, 7782, 7786, 7796, 7806, 7815, 7818, 7832, 7839, 7842, 7856, 7861, 7867, 7878, 7883, 7895, 7901, 7908, 7915, 7921, 7934, 7942, 7951, 7958, 7963, 7973, 7979, 7986, 7998, 8004, 8012, 8017, 8031, 8039, 8045, 8053, 8061, 8071, 8076, 8086, 8089, 8098, 8111, 8119, 8128, 8132, 8140, 8145, 8153, 8165, 8171, 8181, 8187, 8199, 8208, 8213, 8222, 8231, 8234, 8243, 8249, 8261, 8268, 8273, 8284, 8295, 8298, 8310, 8320, 8321, 8331, 8343, 8347, 8353, 8368, 8375, 8383, 8388, 8399, 8404, 8409, 8423, 8429, 8439, 8441, 8449, 8458, 8468, 8476, 8481, 8496, 8499, 8509, 8514, 8527, 8533, 8538, 8549, 8558, 8568, 8573, 8581, 8591, 8593, 8603, 8616, 8617, 8625, 8634, 8644, 8655, 8662, 8668, 8680, 8685, 8692, 8701, 8710, 8715, 8723, 8735, 8744, 8752, 8758, 8766, 8770, 8780, 8791, 8797, 8806, 8816, 8818, 8826, 8836, 8847, 8850, 8863, 8870, 8880, 8887, 8890, 8904, 8908, 8914, 8926, 8934, 8940, 8947, 8957, 8967, 8976, 8977, 8989, 8999, 9005, 9014, 9023, 9028, 9033, 9043, 9052, 9063, 9067, 9079, 9081, 9094, 9102, 9106, 9116, 9121, 9129, 9141, 9149, 9157, 9164, 9174, 9184, 9190, 9194, 9202, 9214, 9219, 9229, 9239, 9246, 9252, 9262, 9268, 9280, 9288, 9295, 9297, 9308, 9314, 9326, 9333, 9338, 9350, 9359, 9365, 9375, 9381, 9387, 9394, 9401, 9414, 9422, 9425, 9438, 9445, 9454, 9462, 9472, 9477, 9483, 9491, 9500, 9506, 9515, 9526, 9530, 9543, 9545, 9558, 9562, 9571, 9579, 9592, 9600, 9607, 9613, 9620, 9632, 9637, 9645, 9655, 9663, 9668, 9680, 9685, 9690, 9701, 9711, 9715, 9728, 9733, 9743, 9745, 9757, 9763, 9773, 9783, 9790, 9798, 9806, 9809, 9818, 9831, 9835, 9846, 9850, 9858, 9867, 9877, 9883, 9896, 9904, 9910, 9916, 9926, 9934, 9941, 9947, 9953, 9968, 9976, 9982, 9985, 9998, 10007, 10009, 10024, 10030, 10034, 10047, 10054, 10064, 10068, 10074, 10084, 10092, 10104, 10105, 10114, 10123, 10135, 10141, 10145, 10155, 10164, 10175, 10184, 10190, 10199, 10204, 10214, 10221, 10227, 10238, 10246, 10249, 10258, 10271, 10276, 10282, 10294, 10302, 10309, 10317, 10323, 10331, 10343, 10347, 10358, 10368, 10372, 10383, 10389, 10395, 10405, 10416, 10422, 10427, 10435, 10443, 10449, 10463, 10470, 10474, 10482, 10492, 10504, 10507, 10517, 10528, 10536, 10539, 10551, 10556, 10564, 10575, 10584, 10588, 10597, 10605, 10610, 10623, 10632, 10639, 10644, 10654, 10661, 10671, 10678, 10687, 10695, 10698, 10706, 10719, 10727, 10733, 10738, 10750, 10760, 10764, 10776, 10782, 10785, 10800, 10801, 10815, 10824, 10826, 10839, 10847, 10853, 10862, 10871, 10876, 10882, 10891, 10902, 10908, 10919, 10928, 10936, 10942, 10945, 10957, 10966, 10973, 10981, 10992, 10994, 11006, 11013, 11022, 11025, 11036, 11041, 11056, 11062, 11071, 11074, 11085, 11091, 11098, 11107, 11118, 11126, 11130, 11140, 11151, 11160, 11167, 11169, 11179, 11191, 11200, 11202, 11210, 11219, 11228, 11236, 11246, 11249, 11257, 11270, 11275, 11287, 11292, 11302, 11312, 11314, 11324, 11334, 11339, 11346, 11354, 11368, 11369, 11382, 11391, 11395, 11401, 11413, 11419, 11431, 11438, 11447, 11450, 11463, 11468, 11475, 11488, 11492, 11502, 11505, 11516, 11521, 11530, 11542, 11545, 11559, 11565, 11572, 11582, 11591, 11595, 11607, 11611, 11621, 11631, 11634, 11647, 11652, 11663, 11665, 11680, 11681, 11693, 11697, 11707, 11715, 11728, 11734, 11737, 11751, 11760, 11763, 11772, 11780, 11787, 11795, 11802, 11815, 11821, 11827, 11838, 11841, 11849, 11862, 11866, 11873, 11885, 11895, 11898, 11911, 11914, 11925, 11929, 11942, 11948, 11960, 11964, 11970, 11984, 11986, 11993, 12004, 12016, 12024, 12027, 12035, 12042, 12051, 12059, 12069, 12073, 12083, 12095, 12100, 12106, 12119, 12125, 12136, 12139, 12149, 12154, 12164, 12174, 12181, 12189, 12197, 12201, 12210, 12220, 12231, 12233, 12244, 12250, 12262, 12272, 12277, 12284, 12292, 12300, 12305, 12313, 12325, 12334, 12339, 12351, 12354, 12362, 12372, 12380, 12390, 12396, 12402, 12410, 12420, 12432, 12436, 12442, 12456, 12460, 12466, 12476, 12484, 12492, 12501, 12506, 12513, 12521, 12535, 12542, 12552, 12559, 12566, 12571, 12577, 12586, 12593, 12602, 12610, 12621, 12627, 12637, 12644, 12654, 12660, 12670, 12674, 12683, 12692, 12704, 12711, 12720, 12726, 12729, 12744, 12745, 12756, 12761, 12772, 12781, 12786, 12795, 12802, 12810, 12822, 12831, 12836, 12848, 12855, 12864, 12869, 12879, 12887, 12896, 12898, 12906, 12916, 12925, 12930, 12944, 12952, 12957, 12968, 12975, 12983, 12985, 12994, 13006, 13012, 13022, 13026, 13038, 13041, 13050, 13062, 13066, 13079, 13081, 13091, 13098, 13108, 13114, 13125, 13135, 13140, 13149, 13158, 13166, 13175, 13180, 13190, 13200, 13205, 13210, 13219, 13232, 13240, 13247, 13256, 13258, 13268, 13279, 13285, 13289, 13303, 13311, 13313, 13325, 13336, 13344, 13348, 13357, 13364, 13374, 13380, 13392, 13399, 13402, 13411, 13421, 13430, 13437, 13442, 13454, 13463, 13466, 13474, 13484, 13496, 13502, 13509, 13519, 13523, 13536, 13537, 13546, 13558, 13563, 13575, 13579, 13586, 13594, 13603, 13610, 13623, 13632, 13637, 13648, 13652, 13660, 13671, 13678, 13685, 13694, 13703, 13709, 13717, 13724, 13731, 13740, 13747, 13757, 13767, 13776, 13779, 13789, 13795, 13803, 13813, 13821, 13828, 13836, 13841, 13854, 13861, 13865, 13878, 13883, 13890, 13901, 13906, 13920, 13923, 13933, 13937, 13949, 13954, 13966, 13970, 13979, 13987, 14000, 14005, 14014, 14023, 14027, 14034, 14042, 14052, 14057, 14071, 14080, 14086, 14096, 14098, 14109, 14120, 14123, 14136, 14138, 14152, 14160, 14161, 14170, 14177, 14185, 14199, 14202, 14210, 14219, 14232, 14236, 14247, 14254, 14262, 14269, 14280, 14286, 14293, 14301, 14311, 14318, 14327, 14330, 14329]Reduce the balanced fully crossed design to the original experimental design:
fake_kb07_df= fake_kb07_df[idx, :]
rename!(fake_kb07_df, :dv => :rt_trunc)Now we can use the simulated data in the same way as above.
Set contrasts:
contrasts = Dict(:spkr => HelmertCoding(),
:prec => HelmertCoding(),
:load => HelmertCoding(),
:item => Grouping(),
:subj => Grouping());Dict{Symbol, StatsModels.AbstractContrasts} with 5 entries:
:item => Grouping()
:spkr => HelmertCoding(nothing, nothing)
:load => HelmertCoding(nothing, nothing)
:prec => HelmertCoding(nothing, nothing)
:subj => Grouping()Define formula, same as above:
kb07_f = @formula(rt_trunc ~ 1 + spkr + prec + load + (1|subj) + (1+prec|item));FormulaTerm
Response:
rt_trunc(unknown)
Predictors:
1
spkr(unknown)
prec(unknown)
load(unknown)
(subj)->1 | subj
(prec,item)->(1 + prec) | itemFit the model:
fake_kb07_m = fit(MixedModel, kb07_f, fake_kb07_df; contrasts=contrasts)Linear mixed model fit by maximum likelihood
rt_trunc ~ 1 + spkr + prec + load + (1 | subj) + (1 + prec | item)
logLik -2 logLik AIC AICc BIC
-2547.4924 5094.9849 5112.9849 5113.0859 5162.4047
Variance components:
Column Variance Std.Dev. Corr.
item (Intercept) 0.00003193 0.00565035
prec: maintain 0.00003011 0.00548705 -1.00
subj (Intercept) 0.00028736 0.01695171
Residual 1.00497260 1.00248322
Number of obs: 1792; levels of grouping factors: 32, 56
Fixed-effects parameters:
─────────────────────────────────────────────────────────
Coef. Std. Error z Pr(>|z|)
─────────────────────────────────────────────────────────
(Intercept) -0.0370081 0.0238277 -1.55 0.1204
spkr: old 0.000976525 0.02377 0.04 0.9672
prec: maintain 0.0309072 0.0237777 1.30 0.1937
load: yes 0.0234262 0.0237083 0.99 0.3231
─────────────────────────────────────────────────────────Set random seed for reproducibility:
rng = StableRNG(42);StableRNGs.LehmerRNG(state=0x00000000000000000000000000000055)Then, again, we specify β, σ, and θ. Here we use the values that we found in the model of the existing dataset:
#beta
new_beta = [2181.85, 67.879, -333.791, 78.5904] #manual
new_beta = kb07_m.β #grab from existing model
#sigma
new_sigma = 680.032 #manual
new_sigma = kb07_m.σ #grab from existing model
#theta
re_item_corr = [1.0 -0.7; -0.7 1.0]
re_item = create_re(0.536, 0.371; corrmat = re_item_corr)
re_subj = create_re(0.438)
new_theta = createθ(kb07_m; item=re_item, subj=re_subj)4-element Vector{Float64}:
0.536
-0.2597
0.26494699469893973
0.438Run nsims iterations:
fake_kb07_sim = parametricbootstrap(rng, nsims, fake_kb07_m,
β = new_beta,
σ = new_sigma,
θ = new_theta,
use_threads = false);MixedModels.MixedModelBootstrap{Float64}(NamedTuple{(:objective, :σ, :β, :se, :θ), Tuple{Float64, Float64, NamedTuple{(Symbol("(Intercept)"), Symbol("spkr: old"), Symbol("prec: maintain"), Symbol("load: yes")), NTuple{4, Float64}}, StaticArrays.SVector{4, Float64}, StaticArrays.SVector{4, Float64}}}[(objective = 28669.25918535114, σ = 671.5885156589217, β = ((Intercept) = 2116.423365946339, spkr: old = 90.29598722286697, prec: maintain = 402.53317308525965, load: yes = 91.06728725160691), se = [85.97890839831933, 16.369495338488566, 52.00052380630839, 16.27366120829669], θ = [0.6339049250520841, -0.34410367832253297, 0.23400465367064743, 0.4275482429365515]), (objective = 28748.177553778678, σ = 692.1085844923699, β = ((Intercept) = 2128.074884086738, spkr: old = 76.2281301119925, prec: maintain = 392.9390606414458, load: yes = 85.23151676762672), se = [82.0534017930162, 16.846025244278287, 49.42808540389314, 16.745871634485265], θ = [0.619482679026013, -0.26278852399996383, 0.2747916881797304, 0.2892535736784387]), (objective = 28713.68960706164, σ = 679.6001562511052, β = ((Intercept) = 2263.098981296992, spkr: old = 72.00119769586878, prec: maintain = 300.5134587654282, load: yes = 91.43156164320013), se = [80.39183969051611, 16.570714180533553, 40.03489871808155, 16.47913820276018], θ = [0.5402665754003372, -0.1963676556162446, 0.23191375106768755, 0.49091212110336]), (objective = 28790.93146109082, σ = 701.5602608493942, β = ((Intercept) = 2081.587051013899, spkr: old = 101.08271262389019, prec: maintain = 346.3725102164116, load: yes = 92.07032498318448), se = [65.12308452632485, 17.083870277437846, 45.099572840947296, 16.981638699462987], θ = [0.406099958663549, -0.2589258150951959, 0.21576621487440634, 0.4026410485928822]), (objective = 28732.966853622078, σ = 689.3642187162451, β = ((Intercept) = 2191.7156079369524, spkr: old = 83.61684273106772, prec: maintain = 314.76465072681134, load: yes = 73.44844220267687), se = [71.93577202050243, 16.783413628463098, 45.00663311499633, 16.68644397637482], θ = [0.4945950578051491, -0.27594724406330823, 0.20395263506970165, 0.387176860381281]), (objective = 28702.0047602433, σ = 680.2912991958342, β = ((Intercept) = 2236.5056370618427, spkr: old = 80.93974965740125, prec: maintain = 305.32605192457964, load: yes = 78.0628071387513), se = [66.76292661840604, 16.584980525415638, 39.85147474697569, 16.48864931224924], θ = [0.3731382120000722, -0.1879849883243117, 0.23620923342041586, 0.513676963503442]), (objective = 28691.936077108032, σ = 676.7499956780237, β = ((Intercept) = 2187.416582712957, spkr: old = 72.66509255041814, prec: maintain = 316.1840389360163, load: yes = 97.21128280633634), se = [78.59212445419045, 16.500294810277865, 52.02954464368879, 16.40092323382156], θ = [0.5679570434583623, -0.30256720074787263, 0.2809216178805866, 0.3985895258297072]), (objective = 28676.24706809285, σ = 674.2037690884966, β = ((Intercept) = 2268.56457985681, spkr: old = 52.57223385208904, prec: maintain = 314.7305648985566, load: yes = 68.56523726323555), se = [70.73068361906067, 16.442639076327048, 51.70105044171187, 16.34185380136621], θ = [0.4909499188970905, -0.26774280024521774, 0.31274870518831155, 0.40329515292375623]), (objective = 28725.862416186832, σ = 681.1355468729755, β = ((Intercept) = 2172.6039321755425, spkr: old = 51.96959381836491, prec: maintain = 273.3898634000491, load: yes = 102.54853313683714), se = [77.23798155768898, 16.619413408891116, 49.43804131433721, 16.51997208573777], θ = [0.5297347707290837, -0.2287297199322546, 0.31234985961127726, 0.4439727566928454]), (objective = 28707.118566880716, σ = 679.2393291550802, β = ((Intercept) = 2180.211365717103, spkr: old = 59.53339621287364, prec: maintain = 321.3181651115789, load: yes = 74.37792465349916), se = [80.0888536074278, 16.556605419020837, 37.19883011125159, 16.467883882459603], θ = [0.5427518843216623, -0.17150016507274912, 0.21876356545705, 0.4808660369082259]) … (objective = 28754.193126887076, σ = 688.3845550979433, β = ((Intercept) = 2213.5324730579405, spkr: old = 74.1676207078408, prec: maintain = 303.2450723246382, load: yes = 101.54275174201415), se = [78.59099071855096, 16.784563186565972, 49.75344913975128, 16.68502138363872], θ = [0.5382813659147446, -0.2869376255134538, 0.2571813856824151, 0.4370441160247303]), (objective = 28765.106783726533, σ = 693.6098893165989, β = ((Intercept) = 2227.907360767297, spkr: old = 78.65653618553948, prec: maintain = 248.57776196191298, load: yes = 93.52081924791308), se = [80.04953078936155, 16.891936003314612, 49.644325718152515, 16.793669488930632], θ = [0.5683356211948474, -0.31479252261569923, 0.21488100102401966, 0.3857792610646542]), (objective = 28701.755166729366, σ = 681.6824101410891, β = ((Intercept) = 2143.963265657268, spkr: old = 76.38685339863137, prec: maintain = 318.90734183707775, load: yes = 52.26069954600215), se = [66.04543313577632, 16.616367943510568, 43.28393980030969, 16.51834612081368], θ = [0.4303989668471523, -0.19661516883661345, 0.2677366476186409, 0.41186637732552445]), (objective = 28555.504937838177, σ = 652.4341720449872, β = ((Intercept) = 2098.809036436014, spkr: old = 56.261963771968176, prec: maintain = 380.22052418980064, load: yes = 72.13223373682455), se = [70.92737148466693, 15.905425402712158, 42.750817161488726, 15.81284098231218], θ = [0.502962010462108, -0.2352881013289702, 0.25168895295202537, 0.43276154571125564]), (objective = 28592.39930350668, σ = 661.1915065732131, β = ((Intercept) = 2236.642058373498, spkr: old = 65.57538118463145, prec: maintain = 350.13472745438503, load: yes = 71.90494961822823), se = [67.26353255880728, 16.10156743776934, 38.12294296448869, 16.010772276309968], θ = [0.4126817794722996, -0.23540448661271043, 0.1797313439672104, 0.4997579992247206]), (objective = 28737.867791564106, σ = 686.3562339789033, β = ((Intercept) = 2165.584532859084, spkr: old = 68.19907945532339, prec: maintain = 330.32131804036817, load: yes = 99.92516622621677), se = [79.7369957139054, 16.729903032820953, 50.01840366356137, 16.630687108948933], θ = [0.5718286099614355, -0.2837065131719171, 0.266041286555998, 0.38951088778298143]), (objective = 28826.598971720512, σ = 701.3668188806352, β = ((Intercept) = 2087.768864605674, spkr: old = 73.81094871405423, prec: maintain = 354.3955965781725, load: yes = 91.9505378292766), se = [78.9478437250913, 17.10787031966048, 46.62882317811358, 17.00802730688193], θ = [0.5107714521514054, -0.224531285209741, 0.26893372534128923, 0.47024607554674996]), (objective = 28761.512288452952, σ = 694.4292802991403, β = ((Intercept) = 2251.1096195312866, spkr: old = 57.76798292660433, prec: maintain = 295.8861396271823, load: yes = 69.34637818363497), se = [84.59025118292931, 16.887552339761328, 55.819121599825, 16.78959526045445], θ = [0.6126844891320918, -0.4047768065870377, 0.1558366088424055, 0.3772228927630545]), (objective = 28668.492995053588, σ = 671.1999251606923, β = ((Intercept) = 2121.278803782974, spkr: old = 32.47224073189596, prec: maintain = 368.95936530955095, load: yes = 41.63501184430273), se = [69.70038228466008, 16.376482772653684, 46.15609420856442, 16.27820283352061], θ = [0.43338447437102084, -0.21744096435265559, 0.2921450071828605, 0.4932756726221565]), (objective = 28684.776840479008, σ = 678.2946095044848, β = ((Intercept) = 2127.075198827885, spkr: old = 66.77914930829377, prec: maintain = 359.99510325781944, load: yes = 53.362760302894166), se = [69.82881994048729, 16.530601115795996, 50.040511699542705, 16.429853969171056], θ = [0.5002008890848008, -0.2528760645642175, 0.3025787342593575, 0.3518053183377909])], LinearAlgebra.LowerTriangular{Float64, Matrix{Float64}}[[0.005636349989462335 0.0; -0.00547345729784501 0.0], [0.016909716278290108;;]], [[1, 2, 4], [1]], [0.0, -Inf, 0.0, 0.0], (item = ("(Intercept)", "prec: maintain"), subj = ("(Intercept)",)))Power calculation
power_table(fake_kb07_sim)4-element Vector{NamedTuple{(:coefname, :power), Tuple{String, Float64}}}:
(coefname = "(Intercept)", power = 1.0)
(coefname = "spkr: old", power = 0.99)
(coefname = "prec: maintain", power = 1.0)
(coefname = "load: yes", power = 1.0)Compare to the powertable from the existing data:
power_table(kb07_sim)4-element Vector{NamedTuple{(:coefname, :power), Tuple{String, Float64}}}:
(coefname = "prec: break", power = 1.0)
(coefname = "(Intercept)", power = 1.0)
(coefname = "spkr: old", power = 0.99)
(coefname = "load: yes", power = 1.0)We have successfully recreated the power simulation of an existing dataset from scratch. This has the advantage, that we now can iterate over different numbers of subjects and items.
Loop over subject and item sizes
When designing a study, you may be interested in trying various numbers of subjects and items to see how that affects the power of your study. To do this you can use a loop to run simulations over a range of values for any parameter.
We first define every fixed things outside the loop (same as above):
Define factors in a dict:
subj_btwn = nothing
item_btwn = nothing
both_win = Dict(:spkr => ["old", "new"],
:prec => ["maintain", "break"],
:load => ["yes", "no"]);Dict{Symbol, Vector{String}} with 3 entries:
:spkr => ["old", "new"]
:load => ["yes", "no"]
:prec => ["maintain", "break"]Set contrasts:
contrasts = Dict(:spkr => HelmertCoding(),
:prec => HelmertCoding(base="maintain"),
:load => HelmertCoding());Dict{Symbol, StatsModels.HelmertCoding} with 3 entries:
:spkr => HelmertCoding(nothing, nothing)
:load => HelmertCoding(nothing, nothing)
:prec => HelmertCoding("maintain", nothing)Set random seed for reproducibility:
rng = StableRNG(42);StableRNGs.LehmerRNG(state=0x00000000000000000000000000000055)Define formula:
kb07_f = @formula(rt_trunc ~ 1 + spkr + prec + load + (1 | subj) + (1 + prec | item));FormulaTerm
Response:
rt_trunc(unknown)
Predictors:
1
spkr(unknown)
prec(unknown)
load(unknown)
(subj)->1 | subj
(prec,item)->(1 + prec) | itema Specify β, σ, and θ:
#beta
new_beta = [2181.85, 67.879, -333.791, 78.5904]
new_beta = kb07_m.β
#sigma
new_sigma = 680.032
new_sigma = kb07_m.σ
#theta
re_item_corr = [1.0 -0.7; -0.7 1.0]
re_item = create_re(0.536, 0.371; corrmat = re_item_corr)
re_subj = create_re(0.438)
# because the ordering in theta is dependent on the design,
# we will create it within the loop as we change the design parameters
# (e.g. n subjects and n items)1×1 LinearAlgebra.LowerTriangular{Float64, LinearAlgebra.Diagonal{Float64, Vector{Float64}}}:
0.438Then we define the variables that out loop will iterate over
Define subject and item numbers as arrays:
sub_ns = [20, 30, 40];
item_ns = [16, 24, 32];3-element Vector{Int64}:
16
24
32Make an empty dataframe:
d = DataFrame();Run the loop:
@showprogress for subj_n in sub_ns, item_n in item_ns
# Make balanced fully crossed data:
fake = simdat_crossed(subj_n, item_n;
subj_btwn = subj_btwn,
item_btwn = item_btwn,
both_win = both_win);
fake_df = DataFrame(fake)
# Reduce the balanced fully crossed design to the original experimental design:
fake_df = sort(fake_df, [:subj, :item, :load, :prec, :spkr])
local len = convert(Int64,(length(fake)/8))
local idx = rand(rng, collect(1:8) , len)
local A = repeat([8], inner=len-1)
push!(A, 0)
A = cumsum(A)
idx = idx + A
fake_df = fake_df[idx, :]
rename!(fake_df, :dv => :rt_trunc)
# create the model:
fake_m = LinearMixedModel(kb07_f, fake_df, contrasts=contrasts);
local new_theta = createθ(fake_m; item=re_item, subj=re_subj)
# Run nsims iterations:
fake_sim = parametricbootstrap(rng, nsims, fake_m,
β = new_beta,
σ = new_sigma,
θ = new_theta,
use_threads = false,
hide_progress=true);
# Power calculation
local ptbl = power_table(fake_sim)
ptdf = DataFrame(ptbl)
ptdf[!, :item_n] .= item_n
ptdf[!, :subj_n] .= subj_n
append!(d, ptdf)
end
Progress: 67%|███████████████████████████▍ | ETA: 0:00:02
Progress: 100%|█████████████████████████████████████████| Time: 0:00:04Our dataframe d now contains the power information for each combination of subjects and items.
first(d, 10)10 rows × 4 columns
| coefname | power | item_n | subj_n | |
|---|---|---|---|---|
| String | Float64 | Int64 | Int64 | |
| 1 | prec: break | 0.99 | 16 | 20 |
| 2 | (Intercept) | 1.0 | 16 | 20 |
| 3 | spkr: old | 0.43 | 16 | 20 |
| 4 | load: yes | 0.49 | 16 | 20 |
| 5 | prec: break | 1.0 | 24 | 20 |
| 6 | (Intercept) | 1.0 | 24 | 20 |
| 7 | spkr: old | 0.59 | 24 | 20 |
| 8 | load: yes | 0.63 | 24 | 20 |
| 9 | prec: break | 1.0 | 32 | 20 |
| 10 | (Intercept) | 1.0 | 32 | 20 |
Lastly we plot our results:
function subplot_power(f::Figure, dat, coefname)
coefpow = @subset(dat, :coefname == coefname)
ax = Axis(f;
xlabel="n subjects",
ylabel="n items",
#aspect=AxisAspect(1),
title="$(coefname)")
heatmap!(ax, coefpow.subj_n, coefpow.item_n, coefpow.power; colorrange=[0,1])
return ax
end
fig = Figure(; resolution=(1300,300))
for (idx, cn) in enumerate(sort(unique(d.coefname)))
fig[1, idx] = subplot_power(fig, d, cn)
end
Colorbar(fig[1, end+1]; label="power", vertical=true, colorrange=[0,1], colormap=:viridis)
figAcknowledgements
The text here is based on a tutorial presented at a ZiF workshop by Lisa DeBruine (Feb. 2020) and presented again by Phillip Alday during the SMLP Summer School (Sep. 2020).
Updated and extended by Lisa Schwetlick & Daniel Backhaus, with the kind help of Phillip Alday, after changes to the package.