Kliegl et al. (2015) is a follow-up to Kliegl et al. (2011) (see also script kwdyz11.qmd) from an experiment looking at a variety of effects of visual cueing under four different cue-target relations (CTRs). In this experiment two rectangles are displayed (1) in horizontal orientation , (2) in vertical orientation, (3) in left diagonal orientation, or in (4) right diagonal orientation relative to a central fixation point. Subjects react to the onset of a small or a large visual target occurring at one of the four ends of the two rectangles. The target is cued validly on 70% of trials by a brief flash of the corner of the rectangle at which it appears; it is cued invalidly at the three other locations 10% of the trials each. This implies a latent imbalance in design that is not visible in the repeated-measures ANOVA, but we will show its effect in the random-effect structure and conditional modes.
There are a couple of differences between the first and this follow-up experiment, rendering it more a conceptual than a direct replication. First, the original experiment was carried out at Peking University and this follow-up at Potsdam University. Second, diagonal orientations of rectangles and large target sizes were not part of the design of Kliegl et al. (2011).
We specify three contrasts for the four-level factor CTR that are derived from spatial, object-based, and attractor-like features of attention. They map onto sequential differences between appropriately ordered factor levels. Replicating Kliegl et al. (2011), the attraction effect was not significant as a fixed effect, but yielded a highly reliable variance component (VC; i.e., reliable individual differences in positive and negative attraction effects cancel the fixed effect). Moreover, these individual differences in the attraction effect were negatively correlated with those in the spatial effect.
This comparison is of interest because a few years after the publication of Kliegl et al. (2011), the theoretically critical correlation parameter (CP) between the spatial effect and the attraction effect was determined as the source of a non-singular LMM in that paper. The present study served the purpose to estimate this parameter with a larger sample and a wider variety of experimental conditions.
Here we also include two additional experimental manipulations of target size and orientation of cue rectangle. A similar analysis was reported in the parsimonious mixed-model paper (Bates et al., 2015); it was also used in a paper of GAMMs (Baayen et al., 2017). Data and R scripts of those analyses are also available in R-package RePsychLing.
The analysis is based on log-transformed reaction times lrt, indicated by a boxcox() check of model residuals.
In this vignette we focus on the reduction of model complexity. And we start with a quote:
“Neither the [maximal] nor the [minimal] linear mixed models are appropriate for most repeated measures analysis. Using the [maximal] model is generally wasteful and costly in terms of statiscal power for testing hypotheses. On the other hand, the [minimal] model fails to account for nontrivial correlation among repeated measurements. This results in inflated [T]ype I error rates when non-negligible correlation does in fact exist. We can usually find middle ground, a covariance model that adequately accounts for correlation but is more parsimonious than the [maximal] model. Doing so allows us full control over [T]ype I error rates without needlessly sacrificing power.”
Stroup, W. W. (2012, p. 185). Generalized linear mixed models: Modern concepts, methods and applica?ons. CRC Press, Boca Raton.
using Arrow
using AlgebraOfGraphics
using AlgebraOfGraphics: density
using BoxCox
using CairoMakie
using CategoricalArrays
using Chain
using DataFrameMacros
using DataFrames
using MixedModels
using MixedModelsMakie
using ProgressMeter
using Random
using SMLP2023: dataset
using StatsBase
ProgressMeter.ijulia_behavior(:clear)
CairoMakie.activate!(; type="svg")dat = DataFrame(dataset(:kkl15))
describe(dat)| Row | variable | mean | min | median | max | nmissing | eltype |
|---|---|---|---|---|---|---|---|
| Symbol | Union… | Any | Union… | Any | Int64 | DataType | |
| 1 | Subj | S001 | S147 | 0 | String | ||
| 2 | CTR | dod | val | 0 | String | ||
| 3 | rt | 293.147 | 150.22 | 276.594 | 749.481 | 0 | Float32 |
| 4 | cardinal | cardinal | diagonal | 0 | String | ||
| 5 | size | big | small | 0 | String |
dat_subj = combine(
groupby(dat, [:Subj, :CTR]),
nrow => :n,
:rt => mean => :rt_m,
:rt => (c -> mean(log, c)) => :lrt_m,
)
dat_subj.CTR = categorical(dat_subj.CTR, levels=levels(dat.CTR))
describe(dat_subj)| Row | variable | mean | min | median | max | nmissing | eltype |
|---|---|---|---|---|---|---|---|
| Symbol | Union… | Any | Union… | Any | Int64 | DataType | |
| 1 | Subj | S001 | S147 | 0 | String | ||
| 2 | CTR | val | dod | 0 | CategoricalValue{String, UInt32} | ||
| 3 | n | 156.294 | 49 | 64.0 | 448 | 0 | Int64 |
| 4 | rt_m | 308.223 | 208.194 | 304.862 | 584.71 | 0 | Float32 |
| 5 | lrt_m | 5.6908 | 5.33226 | 5.69848 | 6.36141 | 0 | Float32 |
boxplot(
dat_subj.CTR.refs,
dat_subj.lrt_m;
orientation=:horizontal,
show_notch=true,
axis=(;
yticks=(
1:4,
[
"valid cue",
"same obj/diff pos",
"diff obj/same pos",
"diff obj/diff pos",
]
)
),
figure=(; resolution=(800, 300)),
)
Mean of log reaction times for four cue-target relations. Targets appeared at (a) the cued position (valid) in a rectangle, (b) in the same rectangle cue, but at its other end, (c) on the second rectangle, but at a corresponding horizontal/vertical physical distance, or (d) at the other end of the second rectangle, that is \(\sqrt{2}\) of horizontal/vertical distance diagonally across from the cue, that is also at larger physical distance compared to (c).
We remove the outlier subject and replot, but we model the data points in dat and check whether this subject appears as an outlier in the caterpillar plot of conditional modes.
let dat_subj = filter(r -> r.rt_m < 510, dat_subj)
boxplot(
dat_subj.CTR.refs,
dat_subj.lrt_m;
orientation=:horizontal,
show_notch=true,
axis=(;
yticks=(
1:4,
[
"valid cue",
"same obj/diff pos",
"diff obj/same pos",
"diff obj/diff pos",
]
)
),
figure=(; resolution=(800, 300)),
)
end
contrasts = Dict(
:Subj => Grouping(),
:CTR => SeqDiffCoding(; levels=["val", "sod", "dos", "dod"]),
:cardinal => EffectsCoding(; levels=["cardinal", "diagonal"]),
:size => EffectsCoding(; levels=["big", "small"])
)Dict{Symbol, StatsModels.AbstractContrasts} with 4 entries:
:CTR => SeqDiffCoding(["val", "sod", "dos", "dod"])
:size => EffectsCoding(nothing, ["big", "small"])
:Subj => Grouping()
:cardinal => EffectsCoding(nothing, ["cardinal", "diagonal"])m_max_rt = let
form = @formula rt ~ 1 + CTR * size * cardinal +
(1 + CTR * size * cardinal | Subj)
fit(MixedModel, form, dat; contrasts)
endMinimizing 3872 Time: 0:00:06 ( 1.59 ms/it)
objective: 599297.6610000695| Est. | SE | z | p | σ_Subj | |
|---|---|---|---|---|---|
| (Intercept) | 308.4078 | 5.8365 | 52.84 | <1e-99 | 0.0000 |
| CTR: sod | 23.2685 | 2.5676 | 9.06 | <1e-18 | 9.9631 |
| CTR: dos | 13.0802 | 1.5433 | 8.48 | <1e-16 | 5.0118 |
| CTR: dod | 2.7724 | 2.0921 | 1.33 | 0.1851 | 13.1147 |
| size: small | 26.4130 | 5.8365 | 4.53 | <1e-05 | 54.0095 |
| cardinal: diagonal | 6.6749 | 1.7890 | 3.73 | 0.0002 | 9.7692 |
| CTR: sod & size: small | 8.7924 | 2.5676 | 3.42 | 0.0006 | 19.8731 |
| CTR: dos & size: small | -0.7061 | 1.5433 | -0.46 | 0.6473 | 7.2502 |
| CTR: dod & size: small | 7.4980 | 2.0921 | 3.58 | 0.0003 | 8.7387 |
| CTR: sod & cardinal: diagonal | 3.6315 | 1.1022 | 3.29 | 0.0010 | 4.2292 |
| CTR: dos & cardinal: diagonal | 1.3344 | 1.2450 | 1.07 | 0.2838 | 1.7717 |
| CTR: dod & cardinal: diagonal | -0.2247 | 1.3224 | -0.17 | 0.8651 | 4.0782 |
| size: small & cardinal: diagonal | 2.0502 | 1.7890 | 1.15 | 0.2518 | 12.9327 |
| CTR: sod & size: small & cardinal: diagonal | -0.7638 | 1.1022 | -0.69 | 0.4883 | 3.7198 |
| CTR: dos & size: small & cardinal: diagonal | -0.1556 | 1.2450 | -0.12 | 0.9005 | 1.7390 |
| CTR: dod & size: small & cardinal: diagonal | 4.1768 | 1.3224 | 3.16 | 0.0016 | 2.3972 |
| Residual | 63.0091 |
m_cpx_rt = let
form = @formula rt ~ 1 + CTR * size * cardinal +
(1 + CTR + size + cardinal | Subj)
fit(MixedModel, form, dat; contrasts)
endMinimizing 770 Time: 0:00:00 ( 0.25 ms/it)| Est. | SE | z | p | σ_Subj | |
|---|---|---|---|---|---|
| (Intercept) | 308.4074 | 6.0527 | 50.95 | <1e-99 | 40.4433 |
| CTR: sod | 23.2723 | 2.4739 | 9.41 | <1e-20 | 21.2925 |
| CTR: dos | 13.1099 | 1.4621 | 8.97 | <1e-18 | 7.5060 |
| CTR: dod | 2.7140 | 1.9182 | 1.41 | 0.1571 | 13.7125 |
| size: small | 26.3865 | 6.0527 | 4.36 | <1e-04 | 38.7600 |
| cardinal: diagonal | 6.6506 | 1.7311 | 3.84 | 0.0001 | 15.6567 |
| CTR: sod & size: small | 8.7956 | 2.4739 | 3.56 | 0.0004 | |
| CTR: dos & size: small | -0.7230 | 1.4621 | -0.49 | 0.6209 | |
| CTR: dod & size: small | 7.4191 | 1.9182 | 3.87 | 0.0001 | |
| CTR: sod & cardinal: diagonal | 3.6414 | 0.9210 | 3.95 | <1e-04 | |
| CTR: dos & cardinal: diagonal | 1.3276 | 1.2176 | 1.09 | 0.2755 | |
| CTR: dod & cardinal: diagonal | -0.3142 | 1.2217 | -0.26 | 0.7970 | |
| size: small & cardinal: diagonal | 2.0470 | 1.7311 | 1.18 | 0.2370 | |
| CTR: sod & size: small & cardinal: diagonal | -0.7611 | 0.9210 | -0.83 | 0.4086 | |
| CTR: dos & size: small & cardinal: diagonal | -0.1334 | 1.2176 | -0.11 | 0.9128 | |
| CTR: dod & size: small & cardinal: diagonal | 4.1115 | 1.2217 | 3.37 | 0.0008 | |
| Residual | 63.1011 |
bc1 = fit(BoxCoxTransformation, m_max_rt)bc2 = fit(BoxCoxTransformation, m_cpx_rt)Minimizing 1191 Time: 0:00:00 ( 0.14 ms/it)Box-Cox transformation
estimated λ: -0.7062
resultant transformation:
y^-0.7 - 1
------------
-0.7boxcoxplot(bc2; conf_level=0.95)Clear evidence for skew. Traditionally, we used log transforms for reaction times. even stronger than log. We stay with log for now. Could try 1/sqrt(rt).
This is the maximum LMM for the design.
m_max = let
form = @formula log(rt) ~ 1 + CTR * size * cardinal +
(1 + CTR * size * cardinal | Subj)
fit(MixedModel, form, dat; contrasts)
endMinimizing 8282 Time: 0:00:13 ( 1.63 ms/it)
objective: -24691.24618930951| Est. | SE | z | p | σ_Subj | |
|---|---|---|---|---|---|
| (Intercept) | 5.6911 | 0.0174 | 327.65 | <1e-99 | 0.0000 |
| CTR: sod | 0.0744 | 0.0078 | 9.52 | <1e-20 | 0.0096 |
| CTR: dos | 0.0408 | 0.0047 | 8.75 | <1e-17 | 0.0135 |
| CTR: dod | 0.0018 | 0.0056 | 0.31 | 0.7553 | 0.0233 |
| size: small | 0.0921 | 0.0174 | 5.30 | <1e-06 | 0.1607 |
| cardinal: diagonal | 0.0205 | 0.0052 | 3.91 | <1e-04 | 0.0261 |
| CTR: sod & size: small | 0.0244 | 0.0078 | 3.12 | 0.0018 | 0.0671 |
| CTR: dos & size: small | -0.0054 | 0.0047 | -1.15 | 0.2492 | 0.0231 |
| CTR: dod & size: small | 0.0183 | 0.0056 | 3.25 | 0.0011 | 0.0320 |
| CTR: sod & cardinal: diagonal | 0.0101 | 0.0032 | 3.12 | 0.0018 | 0.0074 |
| CTR: dos & cardinal: diagonal | 0.0046 | 0.0037 | 1.24 | 0.2149 | 0.0039 |
| CTR: dod & cardinal: diagonal | -0.0054 | 0.0039 | -1.39 | 0.1648 | 0.0082 |
| size: small & cardinal: diagonal | 0.0042 | 0.0052 | 0.80 | 0.4264 | 0.0395 |
| CTR: sod & size: small & cardinal: diagonal | -0.0032 | 0.0032 | -0.98 | 0.3287 | 0.0135 |
| CTR: dos & size: small & cardinal: diagonal | -0.0005 | 0.0037 | -0.14 | 0.8925 | 0.0033 |
| CTR: dod & size: small & cardinal: diagonal | 0.0111 | 0.0039 | 2.85 | 0.0044 | 0.0082 |
| Residual | 0.1902 |
issingular(m_max)trueonly(MixedModels.PCA(m_max))
Principal components based on correlation matrix
(Intercept) … . . . . .
CTR: sod . . . . .
CTR: dos . . . . .
CTR: dod . . . . .
size: small . . . . .
CTR: sod & size: small … . . . . .
CTR: dos & size: small . . . . .
CTR: dod & size: small . . . . .
cardinal: diagonal . . . . .
CTR: sod & cardinal: diagonal . . . . .
CTR: dos & cardinal: diagonal … . . . . .
CTR: dod & cardinal: diagonal 1.0 . . . .
size: small & cardinal: diagonal 0.03 1.0 . . .
CTR: sod & size: small & cardinal: diagonal 0.44 -0.02 1.0 . .
CTR: dos & size: small & cardinal: diagonal 0.75 0.36 0.1 1.0 .
CTR: dod & size: small & cardinal: diagonal … 0.28 -0.05 0.67 -0.13 1.0
Normalized cumulative variances:
[0.3, 0.577, 0.7187, 0.8235, 0.9131, 0.9482, 0.9806, 0.9983, 0.9997, 0.9999, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0]
Component loadings
… PC13 PC14 PC15 PC16
(Intercept) -0.0 -0.0 0.0 -1.0
CTR: sod -0.03 0.07 -0.02 0.0
CTR: dos 0.41 0.2 0.12 -0.0
CTR: dod -0.02 -0.25 0.29 0.0
size: small … 0.06 -0.26 -0.47 -0.0
CTR: sod & size: small 0.15 0.49 -0.11 -0.0
CTR: dos & size: small 0.41 0.36 0.24 -0.0
CTR: dod & size: small -0.16 -0.35 0.47 0.0
cardinal: diagonal -0.3 0.16 0.1 0.0
CTR: sod & cardinal: diagonal … 0.11 -0.06 0.04 -0.0
CTR: dos & cardinal: diagonal -0.04 -0.33 -0.17 0.0
CTR: dod & cardinal: diagonal -0.32 0.11 -0.05 0.0
size: small & cardinal: diagonal -0.37 0.26 0.11 -0.0
CTR: sod & size: small & cardinal: diagonal 0.21 -0.14 0.16 -0.0
CTR: dos & size: small & cardinal: diagonal … 0.35 -0.2 -0.4 0.0
CTR: dod & size: small & cardinal: diagonal -0.32 0.22 -0.39 0.0VarCorr(m_max)| Column | Variance | Std.Dev | Corr. | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Subj | (Intercept) | 0.00000000 | 0.00000000 | |||||||||||||||
| CTR: sod | 0.00009280 | 0.00963318 | +NaN | |||||||||||||||
| CTR: dos | 0.00018297 | 0.01352646 | +NaN | -0.01 | ||||||||||||||
| CTR: dod | 0.00054215 | 0.02328402 | +NaN | +0.51 | -0.35 | |||||||||||||
| size: small | 0.02583099 | 0.16072022 | +NaN | +0.90 | +0.19 | +0.67 | ||||||||||||
| CTR: sod & size: small | 0.00449651 | 0.06705605 | +NaN | +0.10 | +0.32 | +0.55 | +0.50 | |||||||||||
| CTR: dos & size: small | 0.00053188 | 0.02306260 | +NaN | +0.26 | -0.74 | +0.66 | +0.19 | -0.09 | ||||||||||
| CTR: dod & size: small | 0.00102251 | 0.03197673 | +NaN | +0.40 | +0.45 | +0.49 | +0.68 | +0.70 | +0.15 | |||||||||
| cardinal: diagonal | 0.00068321 | 0.02613836 | +NaN | +0.14 | -0.55 | +0.06 | -0.07 | -0.23 | +0.14 | -0.49 | ||||||||
| CTR: sod & cardinal: diagonal | 0.00005543 | 0.00744533 | +NaN | +0.25 | -0.30 | -0.25 | -0.01 | -0.43 | +0.05 | -0.32 | +0.25 | |||||||
| CTR: dos & cardinal: diagonal | 0.00001502 | 0.00387533 | +NaN | -0.79 | +0.30 | -0.18 | -0.48 | +0.40 | -0.31 | +0.02 | -0.34 | -0.42 | ||||||
| CTR: dod & cardinal: diagonal | 0.00006782 | 0.00823543 | +NaN | +0.35 | -0.55 | +0.34 | +0.14 | -0.36 | +0.83 | +0.17 | +0.02 | +0.24 | -0.59 | |||||
| size: small & cardinal: diagonal | 0.00156110 | 0.03951070 | +NaN | -0.02 | +0.06 | +0.09 | +0.07 | -0.06 | +0.24 | +0.09 | -0.49 | +0.10 | +0.29 | +0.03 | ||||
| CTR: sod & size: small & cardinal: diagonal | 0.00018092 | 0.01345048 | +NaN | +0.28 | -0.08 | +0.15 | +0.26 | +0.04 | +0.28 | +0.35 | -0.21 | -0.13 | -0.33 | +0.44 | -0.02 | |||
| CTR: dos & size: small & cardinal: diagonal | 0.00001090 | 0.00330194 | +NaN | +0.09 | -0.75 | +0.38 | -0.06 | -0.36 | +0.91 | -0.10 | +0.26 | +0.20 | -0.23 | +0.75 | +0.36 | +0.10 | ||
| CTR: dod & size: small & cardinal: diagonal | 0.00006649 | 0.00815442 | +NaN | +0.23 | +0.34 | +0.37 | +0.47 | +0.55 | +0.17 | +0.87 | -0.56 | -0.43 | -0.01 | +0.28 | -0.05 | +0.67 | -0.13 | |
| Residual | 0.03617587 | 0.19019955 |
Force CPs to zero.
m_zcp1 = let
form = @formula log(rt) ~ 1 + CTR * size * cardinal +
zerocorr(1 + CTR * size * cardinal | Subj)
fit(MixedModel, form, dat; contrasts)
endMinimizing 637 Time: 0:00:00 ( 0.32 ms/it)
objective: -24588.607469898558| Est. | SE | z | p | σ_Subj | |
|---|---|---|---|---|---|
| (Intercept) | 5.6910 | 0.0173 | 329.51 | <1e-99 | 0.0151 |
| CTR: sod | 0.0744 | 0.0077 | 9.66 | <1e-21 | 0.0109 |
| CTR: dos | 0.0409 | 0.0045 | 9.09 | <1e-19 | 0.0240 |
| CTR: dod | 0.0015 | 0.0053 | 0.29 | 0.7749 | 0.0299 |
| size: small | 0.0921 | 0.0173 | 5.33 | <1e-07 | 0.1591 |
| cardinal: diagonal | 0.0204 | 0.0052 | 3.92 | <1e-04 | 0.0312 |
| CTR: sod & size: small | 0.0244 | 0.0077 | 3.17 | 0.0015 | 0.0657 |
| CTR: dos & size: small | -0.0053 | 0.0045 | -1.19 | 0.2344 | 0.0010 |
| CTR: dod & size: small | 0.0181 | 0.0053 | 3.39 | 0.0007 | 0.0196 |
| CTR: sod & cardinal: diagonal | 0.0101 | 0.0033 | 3.03 | 0.0025 | 0.0172 |
| CTR: dos & cardinal: diagonal | 0.0046 | 0.0037 | 1.26 | 0.2092 | 0.0000 |
| CTR: dod & cardinal: diagonal | -0.0055 | 0.0037 | -1.49 | 0.1358 | 0.0033 |
| size: small & cardinal: diagonal | 0.0041 | 0.0052 | 0.79 | 0.4291 | 0.0354 |
| CTR: sod & size: small & cardinal: diagonal | -0.0032 | 0.0033 | -0.95 | 0.3427 | 0.0008 |
| CTR: dos & size: small & cardinal: diagonal | -0.0005 | 0.0037 | -0.13 | 0.8945 | 0.0000 |
| CTR: dod & size: small & cardinal: diagonal | 0.0109 | 0.0037 | 2.94 | 0.0033 | 0.0010 |
| Residual | 0.1903 |
issingular(m_zcp1)trueonly(MixedModels.PCA(m_zcp1))
Principal components based on correlation matrix
(Intercept) … . . . . . . .
CTR: sod . . . . . . .
CTR: dos . . . . . . .
CTR: dod . . . . . . .
size: small . . . . . . .
CTR: sod & size: small … . . . . . . .
CTR: dos & size: small . . . . . . .
CTR: dod & size: small . . . . . . .
cardinal: diagonal . . . . . . .
CTR: sod & cardinal: diagonal 1.0 . . . . . .
CTR: dos & cardinal: diagonal … 0.0 0.0 . . . . .
CTR: dod & cardinal: diagonal 0.0 0.0 1.0 . . . .
size: small & cardinal: diagonal 0.0 0.0 0.0 1.0 . . .
CTR: sod & size: small & cardinal: diagonal 0.0 0.0 0.0 0.0 1.0 . .
CTR: dos & size: small & cardinal: diagonal 0.0 0.0 0.0 0.0 0.0 0.0 .
CTR: dod & size: small & cardinal: diagonal … 0.0 0.0 0.0 0.0 0.0 0.0 1.0
Normalized cumulative variances:
[0.0714, 0.1429, 0.2143, 0.2857, 0.3571, 0.4286, 0.5, 0.5714, 0.6429, 0.7143, 0.7857, 0.8571, 0.9286, 1.0, 1.0, 1.0]
Component loadings
… PC13 PC14 PC15 PC16
(Intercept) 0.0 0.0 0.0 0.0
CTR: sod 0.0 0.0 0.0 0.0
CTR: dos 0.0 0.0 0.0 0.0
CTR: dod 0.0 0.0 0.0 0.0
size: small … 0.0 0.0 0.0 0.0
CTR: sod & size: small 0.0 0.0 0.0 0.0
CTR: dos & size: small 0.0 0.0 0.0 0.0
CTR: dod & size: small 1.0 0.0 0.0 0.0
cardinal: diagonal 0.0 1.0 0.0 0.0
CTR: sod & cardinal: diagonal … 0.0 0.0 0.0 0.0
CTR: dos & cardinal: diagonal 0.0 0.0 NaN 0.0
CTR: dod & cardinal: diagonal 0.0 0.0 0.0 0.0
size: small & cardinal: diagonal 0.0 0.0 0.0 0.0
CTR: sod & size: small & cardinal: diagonal 0.0 0.0 0.0 0.0
CTR: dos & size: small & cardinal: diagonal … 0.0 0.0 0.0 NaN
CTR: dod & size: small & cardinal: diagonal 0.0 0.0 0.0 0.0VarCorr(m_zcp1)| Column | Variance | Std.Dev | Corr. | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Subj | (Intercept) | 0.000228119 | 0.015103595 | |||||||||||||||
| CTR: sod | 0.000118184 | 0.010871228 | . | |||||||||||||||
| CTR: dos | 0.000577145 | 0.024023842 | . | . | ||||||||||||||
| CTR: dod | 0.000894364 | 0.029905924 | . | . | . | |||||||||||||
| size: small | 0.025310609 | 0.159093081 | . | . | . | . | ||||||||||||
| CTR: sod & size: small | 0.004316747 | 0.065701959 | . | . | . | . | . | |||||||||||
| CTR: dos & size: small | 0.000000926 | 0.000962365 | . | . | . | . | . | . | ||||||||||
| CTR: dod & size: small | 0.000383055 | 0.019571794 | . | . | . | . | . | . | . | |||||||||
| cardinal: diagonal | 0.000972318 | 0.031182012 | . | . | . | . | . | . | . | . | ||||||||
| CTR: sod & cardinal: diagonal | 0.000294448 | 0.017159499 | . | . | . | . | . | . | . | . | . | |||||||
| CTR: dos & cardinal: diagonal | 0.000000000 | 0.000000000 | . | . | . | . | . | . | . | . | . | . | ||||||
| CTR: dod & cardinal: diagonal | 0.000010975 | 0.003312812 | . | . | . | . | . | . | . | . | . | . | . | |||||
| size: small & cardinal: diagonal | 0.001254094 | 0.035413184 | . | . | . | . | . | . | . | . | . | . | . | . | ||||
| CTR: sod & size: small & cardinal: diagonal | 0.000000719 | 0.000847671 | . | . | . | . | . | . | . | . | . | . | . | . | . | |||
| CTR: dos & size: small & cardinal: diagonal | 0.000000000 | 0.000000000 | . | . | . | . | . | . | . | . | . | . | . | . | . | . | ||
| CTR: dod & size: small & cardinal: diagonal | 0.000001038 | 0.001019064 | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | |
| Residual | 0.036196631 | 0.190254123 |
Take out VC for interactions.
m_zcp1_rdc = let
form = @formula log(rt) ~ 1 + CTR * size * cardinal +
zerocorr(1 + CTR + size + cardinal | Subj)
fit(MixedModel, form, dat; contrasts)
end| Est. | SE | z | p | σ_Subj | |
|---|---|---|---|---|---|
| (Intercept) | 5.6911 | 0.0173 | 329.28 | <1e-99 | 0.1569 |
| CTR: sod | 0.0745 | 0.0077 | 9.66 | <1e-21 | 0.0666 |
| CTR: dos | 0.0409 | 0.0045 | 9.09 | <1e-19 | 0.0240 |
| CTR: dod | 0.0015 | 0.0053 | 0.29 | 0.7751 | 0.0357 |
| size: small | 0.0920 | 0.0173 | 5.33 | <1e-06 | 0.0312 |
| cardinal: diagonal | 0.0204 | 0.0053 | 3.88 | 0.0001 | 0.0476 |
| CTR: sod & size: small | 0.0244 | 0.0077 | 3.17 | 0.0015 | |
| CTR: dos & size: small | -0.0054 | 0.0045 | -1.20 | 0.2317 | |
| CTR: dod & size: small | 0.0181 | 0.0053 | 3.39 | 0.0007 | |
| CTR: sod & cardinal: diagonal | 0.0101 | 0.0028 | 3.64 | 0.0003 | |
| CTR: dos & cardinal: diagonal | 0.0046 | 0.0037 | 1.25 | 0.2125 | |
| CTR: dod & cardinal: diagonal | -0.0056 | 0.0037 | -1.51 | 0.1317 | |
| size: small & cardinal: diagonal | 0.0042 | 0.0053 | 0.79 | 0.4286 | |
| CTR: sod & size: small & cardinal: diagonal | -0.0031 | 0.0028 | -1.12 | 0.2610 | |
| CTR: dos & size: small & cardinal: diagonal | -0.0005 | 0.0037 | -0.12 | 0.9023 | |
| CTR: dod & size: small & cardinal: diagonal | 0.0109 | 0.0037 | 2.95 | 0.0032 | |
| Residual | 0.1904 |
issingular(m_zcp1_rdc)falseonly(MixedModels.PCA(m_zcp1_rdc))
Principal components based on correlation matrix
(Intercept) 1.0 . . . . .
CTR: sod 0.0 1.0 . . . .
CTR: dos 0.0 0.0 1.0 . . .
CTR: dod 0.0 0.0 0.0 1.0 . .
size: small 0.0 0.0 0.0 0.0 1.0 .
cardinal: diagonal 0.0 0.0 0.0 0.0 0.0 1.0
Normalized cumulative variances:
[0.1667, 0.3333, 0.5, 0.6667, 0.8333, 1.0]
Component loadings
PC1 PC2 PC3 PC4 PC5 PC6
(Intercept) 1.0 0.0 0.0 0.0 0.0 0.0
CTR: sod 0.0 1.0 0.0 0.0 0.0 0.0
CTR: dos 0.0 0.0 1.0 0.0 0.0 0.0
CTR: dod 0.0 0.0 0.0 1.0 0.0 0.0
size: small 0.0 0.0 0.0 0.0 1.0 0.0
cardinal: diagonal 0.0 0.0 0.0 0.0 0.0 1.0VarCorr(m_zcp1_rdc)| Column | Variance | Std.Dev | Corr. | |||||
|---|---|---|---|---|---|---|---|---|
| Subj | (Intercept) | 0.0246022 | 0.1568508 | |||||
| CTR: sod | 0.0044408 | 0.0666395 | . | |||||
| CTR: dos | 0.0005763 | 0.0240065 | . | . | ||||
| CTR: dod | 0.0012752 | 0.0357098 | . | . | . | |||
| size: small | 0.0009731 | 0.0311946 | . | . | . | . | ||
| cardinal: diagonal | 0.0022679 | 0.0476222 | . | . | . | . | . | |
| Residual | 0.0362601 | 0.1904207 |
Let’s compare the three models.
gof_summary = let
nms = [:m_zcp1_rdc, :m_zcp1, :m_max]
mods = eval.(nms)
lrt = MixedModels.likelihoodratiotest(m_zcp1_rdc, m_zcp1, m_max)
DataFrame(;
name = nms,
dof=dof.(mods),
deviance=round.(deviance.(mods), digits=0),
AIC=round.(aic.(mods),digits=0),
AICc=round.(aicc.(mods),digits=0),
BIC=round.(bic.(mods),digits=0),
χ²=vcat(:., round.(lrt.tests.deviancediff, digits=0)),
χ²_dof=vcat(:., round.(lrt.tests.dofdiff, digits=0)),
pvalue=vcat(:., round.(lrt.tests.pvalues, digits=3))
)
end| Row | name | dof | deviance | AIC | AICc | BIC | χ² | χ²_dof | pvalue |
|---|---|---|---|---|---|---|---|---|---|
| Symbol | Int64 | Float64 | Float64 | Float64 | Float64 | Any | Any | Any | |
| 1 | m_zcp1_rdc | 23 | -24558.0 | -24512.0 | -24512.0 | -24308.0 | . | . | . |
| 2 | m_zcp1 | 33 | -24589.0 | -24523.0 | -24523.0 | -24229.0 | 30.0 | 10.0 | 0.001 |
| 3 | m_max | 153 | -24691.0 | -24385.0 | -24384.0 | -23025.0 | 103.0 | 120.0 | 0.872 |
Extend zcp-reduced LMM with CPs
m_prm1 = let
form = @formula log(rt) ~ 1 + CTR * size * cardinal +
(1 + CTR + size + cardinal | Subj)
fit(MixedModel, form, dat; contrasts)
endMinimizing 801 Time: 0:00:00 ( 0.18 ms/it)| Est. | SE | z | p | σ_Subj | |
|---|---|---|---|---|---|
| (Intercept) | 5.6911 | 0.0176 | 323.61 | <1e-99 | 0.1181 |
| CTR: sod | 0.0745 | 0.0076 | 9.75 | <1e-21 | 0.0660 |
| CTR: dos | 0.0408 | 0.0043 | 9.42 | <1e-20 | 0.0213 |
| CTR: dod | 0.0017 | 0.0051 | 0.34 | 0.7374 | 0.0326 |
| size: small | 0.0921 | 0.0176 | 5.23 | <1e-06 | 0.1119 |
| cardinal: diagonal | 0.0204 | 0.0053 | 3.88 | 0.0001 | 0.0476 |
| CTR: sod & size: small | 0.0244 | 0.0076 | 3.19 | 0.0014 | |
| CTR: dos & size: small | -0.0054 | 0.0043 | -1.24 | 0.2156 | |
| CTR: dod & size: small | 0.0181 | 0.0051 | 3.55 | 0.0004 | |
| CTR: sod & cardinal: diagonal | 0.0101 | 0.0028 | 3.64 | 0.0003 | |
| CTR: dos & cardinal: diagonal | 0.0046 | 0.0037 | 1.25 | 0.2118 | |
| CTR: dod & cardinal: diagonal | -0.0056 | 0.0037 | -1.51 | 0.1301 | |
| size: small & cardinal: diagonal | 0.0042 | 0.0053 | 0.79 | 0.4272 | |
| CTR: sod & size: small & cardinal: diagonal | -0.0031 | 0.0028 | -1.13 | 0.2597 | |
| CTR: dos & size: small & cardinal: diagonal | -0.0005 | 0.0037 | -0.13 | 0.8997 | |
| CTR: dod & size: small & cardinal: diagonal | 0.0110 | 0.0037 | 2.98 | 0.0029 | |
| Residual | 0.1904 |
issingular(m_prm1)falseonly(MixedModels.PCA(m_prm1))
Principal components based on correlation matrix
(Intercept) 1.0 . . . . .
CTR: sod 0.64 1.0 . . . .
CTR: dos 0.16 -0.08 1.0 . . .
CTR: dod 0.79 0.6 0.28 1.0 . .
size: small -0.42 -0.16 -0.12 -0.03 1.0 .
cardinal: diagonal 0.05 -0.05 -0.02 0.05 0.08 1.0
Normalized cumulative variances:
[0.414, 0.5967, 0.772, 0.926, 0.9822, 1.0]
Component loadings
PC1 PC2 PC3 PC4 PC5 PC6
(Intercept) -0.6 0.0 0.03 0.12 -0.37 -0.7
CTR: sod -0.5 -0.26 0.31 -0.11 0.76 0.02
CTR: dos -0.16 0.52 -0.72 -0.23 0.34 -0.11
CTR: dod -0.55 -0.18 -0.2 -0.27 -0.4 0.63
size: small 0.25 -0.59 -0.23 -0.66 -0.03 -0.32
cardinal: diagonal -0.0 -0.53 -0.54 0.64 0.12 0.03VarCorr(m_prm1)| Column | Variance | Std.Dev | Corr. | |||||
|---|---|---|---|---|---|---|---|---|
| Subj | (Intercept) | 0.0139568 | 0.1181388 | |||||
| CTR: sod | 0.0043556 | 0.0659971 | +0.64 | |||||
| CTR: dos | 0.0004536 | 0.0212981 | +0.16 | -0.08 | ||||
| CTR: dod | 0.0010640 | 0.0326186 | +0.79 | +0.60 | +0.28 | |||
| size: small | 0.0125269 | 0.1119239 | -0.42 | -0.16 | -0.12 | -0.03 | ||
| cardinal: diagonal | 0.0022690 | 0.0476336 | +0.05 | -0.05 | -0.02 | +0.05 | +0.08 | |
| Residual | 0.0362661 | 0.1904365 |
We note that the critical correlation parameter between spatial (sod) and attraction (dod) is now estimated at .60 – not that close to the 1.0 boundary that caused singularity in Kliegl et al. (2011).
gof_summary = let
nms = [:m_zcp1_rdc, :m_prm1, :m_max]
mods = eval.(nms)
lrt = MixedModels.likelihoodratiotest(m_prm1, m_zcp1, m_max)
DataFrame(;
name = nms,
dof=dof.(mods),
deviance=round.(deviance.(mods), digits=0),
AIC=round.(aic.(mods),digits=0),
AICc=round.(aicc.(mods),digits=0),
BIC=round.(bic.(mods),digits=0),
χ²=vcat(:., round.(lrt.tests.deviancediff, digits=0)),
χ²_dof=vcat(:., round.(lrt.tests.dofdiff, digits=0)),
pvalue=vcat(:., round.(lrt.tests.pvalues, digits=3))
)
end| Row | name | dof | deviance | AIC | AICc | BIC | χ² | χ²_dof | pvalue |
|---|---|---|---|---|---|---|---|---|---|
| Symbol | Int64 | Float64 | Float64 | Float64 | Float64 | Any | Any | Any | |
| 1 | m_zcp1_rdc | 23 | -24558.0 | -24512.0 | -24512.0 | -24308.0 | . | . | . |
| 2 | m_prm1 | 38 | -24615.0 | -24539.0 | -24539.0 | -24201.0 | 27.0 | 5.0 | 0.0 |
| 3 | m_max | 153 | -24691.0 | -24385.0 | -24384.0 | -23025.0 | 76.0 | 115.0 | 0.998 |
Take out interaction VCs.
m_cpx = let
form = @formula log(rt) ~ 1 + CTR * size * cardinal +
(1 + CTR + size + cardinal | Subj)
fit(MixedModel, form, dat; contrasts)
endMinimizing 801 Time: 0:00:00 ( 0.19 ms/it)| Est. | SE | z | p | σ_Subj | |
|---|---|---|---|---|---|
| (Intercept) | 5.6911 | 0.0176 | 323.61 | <1e-99 | 0.1181 |
| CTR: sod | 0.0745 | 0.0076 | 9.75 | <1e-21 | 0.0660 |
| CTR: dos | 0.0408 | 0.0043 | 9.42 | <1e-20 | 0.0213 |
| CTR: dod | 0.0017 | 0.0051 | 0.34 | 0.7374 | 0.0326 |
| size: small | 0.0921 | 0.0176 | 5.23 | <1e-06 | 0.1119 |
| cardinal: diagonal | 0.0204 | 0.0053 | 3.88 | 0.0001 | 0.0476 |
| CTR: sod & size: small | 0.0244 | 0.0076 | 3.19 | 0.0014 | |
| CTR: dos & size: small | -0.0054 | 0.0043 | -1.24 | 0.2156 | |
| CTR: dod & size: small | 0.0181 | 0.0051 | 3.55 | 0.0004 | |
| CTR: sod & cardinal: diagonal | 0.0101 | 0.0028 | 3.64 | 0.0003 | |
| CTR: dos & cardinal: diagonal | 0.0046 | 0.0037 | 1.25 | 0.2118 | |
| CTR: dod & cardinal: diagonal | -0.0056 | 0.0037 | -1.51 | 0.1301 | |
| size: small & cardinal: diagonal | 0.0042 | 0.0053 | 0.79 | 0.4272 | |
| CTR: sod & size: small & cardinal: diagonal | -0.0031 | 0.0028 | -1.13 | 0.2597 | |
| CTR: dos & size: small & cardinal: diagonal | -0.0005 | 0.0037 | -0.13 | 0.8997 | |
| CTR: dod & size: small & cardinal: diagonal | 0.0110 | 0.0037 | 2.98 | 0.0029 | |
| Residual | 0.1904 |
Take out interaction VCs.
m_zcp2 = let
form = @formula log(rt) ~ 1 + CTR * size * cardinal +
zerocorr(1 + CTR + size + cardinal | Subj)
fit(MixedModel, form, dat; contrasts)
end| Est. | SE | z | p | σ_Subj | |
|---|---|---|---|---|---|
| (Intercept) | 5.6911 | 0.0173 | 329.28 | <1e-99 | 0.1569 |
| CTR: sod | 0.0745 | 0.0077 | 9.66 | <1e-21 | 0.0666 |
| CTR: dos | 0.0409 | 0.0045 | 9.09 | <1e-19 | 0.0240 |
| CTR: dod | 0.0015 | 0.0053 | 0.29 | 0.7751 | 0.0357 |
| size: small | 0.0920 | 0.0173 | 5.33 | <1e-06 | 0.0312 |
| cardinal: diagonal | 0.0204 | 0.0053 | 3.88 | 0.0001 | 0.0476 |
| CTR: sod & size: small | 0.0244 | 0.0077 | 3.17 | 0.0015 | |
| CTR: dos & size: small | -0.0054 | 0.0045 | -1.20 | 0.2317 | |
| CTR: dod & size: small | 0.0181 | 0.0053 | 3.39 | 0.0007 | |
| CTR: sod & cardinal: diagonal | 0.0101 | 0.0028 | 3.64 | 0.0003 | |
| CTR: dos & cardinal: diagonal | 0.0046 | 0.0037 | 1.25 | 0.2125 | |
| CTR: dod & cardinal: diagonal | -0.0056 | 0.0037 | -1.51 | 0.1317 | |
| size: small & cardinal: diagonal | 0.0042 | 0.0053 | 0.79 | 0.4286 | |
| CTR: sod & size: small & cardinal: diagonal | -0.0031 | 0.0028 | -1.12 | 0.2610 | |
| CTR: dos & size: small & cardinal: diagonal | -0.0005 | 0.0037 | -0.12 | 0.9023 | |
| CTR: dod & size: small & cardinal: diagonal | 0.0109 | 0.0037 | 2.95 | 0.0032 | |
| Residual | 0.1904 |
gof_summary = let
nms = [:m_zcp2, :m_cpx, :m_max]
mods = eval.(nms)
lrt = MixedModels.likelihoodratiotest(m_zcp2, m_cpx, m_max)
DataFrame(;
name = nms,
dof=dof.(mods),
deviance=round.(deviance.(mods), digits=0),
AIC=round.(aic.(mods),digits=0),
AICc=round.(aicc.(mods),digits=0),
BIC=round.(bic.(mods),digits=0),
χ²=vcat(:., round.(lrt.tests.deviancediff, digits=0)),
χ²_dof=vcat(:., round.(lrt.tests.dofdiff, digits=0)),
pvalue=vcat(:., round.(lrt.tests.pvalues, digits=3))
)
end| Row | name | dof | deviance | AIC | AICc | BIC | χ² | χ²_dof | pvalue |
|---|---|---|---|---|---|---|---|---|---|
| Symbol | Int64 | Float64 | Float64 | Float64 | Float64 | Any | Any | Any | |
| 1 | m_zcp2 | 23 | -24558.0 | -24512.0 | -24512.0 | -24308.0 | . | . | . |
| 2 | m_cpx | 38 | -24615.0 | -24539.0 | -24539.0 | -24201.0 | 57.0 | 15.0 | 0.0 |
| 3 | m_max | 153 | -24691.0 | -24385.0 | -24384.0 | -23025.0 | 76.0 | 115.0 | 0.998 |
We see the model is singular.
issingular(m_cpx_rt)falseMixedModels.PCA(m_cpx_rt)(Subj =
Principal components based on correlation matrix
(Intercept) 1.0 . . . . .
CTR: sod 0.85 1.0 . . . .
CTR: dos 0.56 0.19 1.0 . . .
CTR: dod 0.69 0.54 0.3 1.0 . .
size: small -0.45 -0.23 -0.2 -0.13 1.0 .
cardinal: diagonal -0.07 -0.05 -0.08 0.13 0.2 1.0
Normalized cumulative variances:
[0.465, 0.6637, 0.8016, 0.9245, 0.9964, 1.0]
Component loadings
PC1 PC2 PC3 PC4 PC5 PC6
(Intercept) -0.59 -0.01 -0.02 -0.01 -0.18 -0.79
CTR: sod -0.49 -0.12 -0.43 -0.22 -0.51 0.5
CTR: dos -0.35 0.13 0.87 -0.05 -0.15 0.27
CTR: dod -0.45 -0.36 -0.05 -0.14 0.79 0.17
size: small 0.29 -0.5 0.17 -0.77 -0.15 -0.17
cardinal: diagonal 0.05 -0.77 0.12 0.59 -0.21 0.01,)m_prm1.θ
m_prm1.lowerbd
m_prm1.λ1-element Vector{LinearAlgebra.LowerTriangular{Float64, Matrix{Float64}}}:
[0.6203576608179638 0.0 … 0.0 0.0; 0.22119994699720608 0.26678153140929256 … 0.0 0.0; … ; -0.24965193868875257 0.087476294698932 … 0.4357585158840971 0.0; 0.011471533099315563 -0.0255708216618361 … 0.02800749689407972 0.2461637872603555]Do model residuals meet LMM assumptions? Classic plots are
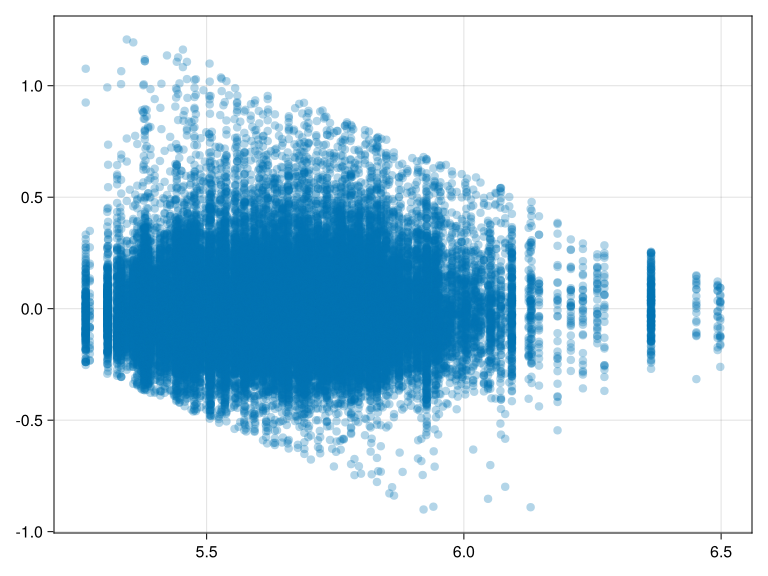
The slant in residuals show a lower and upper boundary of reaction times, that is we have have too few short and too few long residuals. Not ideal, but at least width of the residual band looks similar across the fitted values, that is there is no evidence for heteroskedasticity.
CairoMakie.activate!(; type="png")
scatter(fitted(m_prm1), residuals(m_prm1); alpha=0.3)
With many observations the scatterplot is not that informative. Contour plots or heatmaps may be an alternative.
set_aog_theme!()
draw(
data((; f=fitted(m_prm1), r=residuals(m_prm1))) *
mapping(
:f => "Fitted values from m1", :r => "Residuals from m1"
) *
density();
)
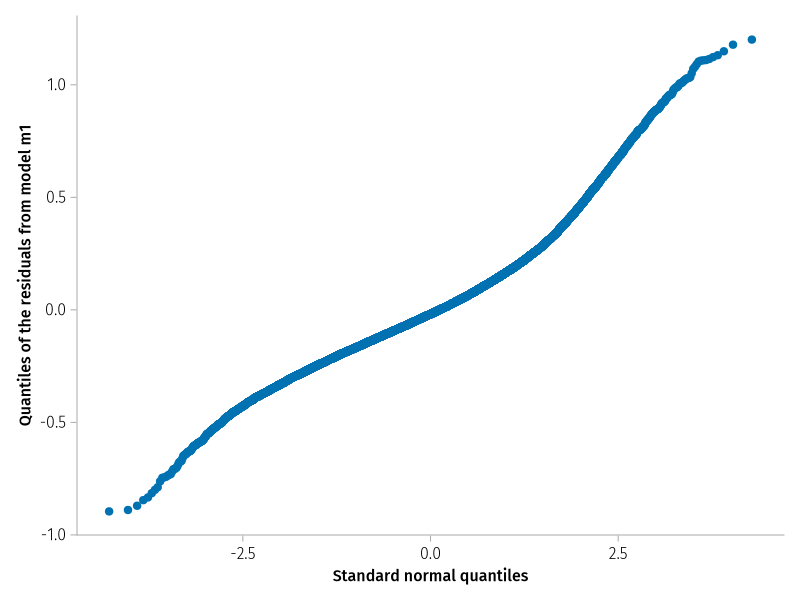
The plot of quantiles of model residuals over corresponding quantiles of the normal distribution should yield a straight line along the main diagonal.
CairoMakie.activate!(; type="png")
qqnorm(
residuals(m_prm1);
qqline=:none,
axis=(;
xlabel="Standard normal quantiles",
ylabel="Quantiles of the residuals from model m1",
),
)
******We****** can see this in this plot. Overall, it does not look too bad.
CairoMakie.activate!(; type="svg")
let
n = nrow(dat)
dat_rz = (;
value=vcat(residuals(m_prm1) ./ std(residuals(m_prm1)), randn(n)),
curve=repeat(["residual", "normal"]; inner=n),
)
draw(
data(dat_rz) *
mapping(:value; color=:curve) *
density(; bandwidth=0.1);
)
end
cm1 = only(ranefinfo(m_prm1))
caterpillar!(Figure(; resolution=(800, 1200)), cm1; orderby=2)
m_prm1)shrinkageplot!(Figure(; resolution=(1000, 1200)), m_prm1)
Here we
We generate 2500 samples for the 15 model parameters (4 fixed effect, 7 VCs, 15 CPs, and 1 residual).
samp = parametricbootstrap(MersenneTwister(1234321), 2500, m_prm1;
optsum_overrides=(; ftol_rel=1e-8));tbl = samp.tblTable with 60 columns and 2500 rows:
obj β01 β02 β03 β04 β05 ⋯
┌────────────────────────────────────────────────────────────────────
1 │ -25123.8 5.68038 0.068683 0.039261 -0.00165125 0.0793335 ⋯
2 │ -24465.9 5.66021 0.0667158 0.0418969 -0.00305185 0.100958 ⋯
3 │ -24446.4 5.6924 0.0778707 0.0369443 0.00797653 0.100114 ⋯
4 │ -24617.7 5.69562 0.0766171 0.0463011 -0.00297233 0.0639383 ⋯
5 │ -25167.8 5.68415 0.0684032 0.0385817 0.00248626 0.118136 ⋯
6 │ -24727.8 5.69527 0.0843717 0.0442493 0.00193816 0.0936532 ⋯
7 │ -24512.0 5.67742 0.0707211 0.0418414 -0.00641572 0.076351 ⋯
8 │ -24798.9 5.69362 0.0765456 0.0458011 0.00328823 0.084062 ⋯
9 │ -24392.5 5.68477 0.0818642 0.0496969 -0.000832281 0.0977178 ⋯
10 │ -24585.7 5.68801 0.0796325 0.0344963 0.00629559 0.081441 ⋯
11 │ -25078.8 5.66697 0.0663796 0.0445354 -0.000736944 0.0943102 ⋯
12 │ -24348.5 5.67785 0.0698993 0.0446523 -0.000859312 0.102561 ⋯
13 │ -24973.2 5.68851 0.0732837 0.0421743 -0.00279674 0.0830709 ⋯
14 │ -24617.9 5.70183 0.07733 0.0433379 -0.00455447 0.0694739 ⋯
15 │ -24775.8 5.68347 0.0825422 0.0371819 0.00388279 0.0889206 ⋯
16 │ -24628.0 5.69649 0.0718965 0.0408693 0.000221452 0.0878074 ⋯
17 │ -24397.7 5.70743 0.0966594 0.0363991 0.00133149 0.087301 ⋯
18 │ -24836.3 5.73132 0.0753929 0.0424585 0.00735246 0.0482915 ⋯
19 │ -24806.7 5.68484 0.0744908 0.0369567 0.0060191 0.0529119 ⋯
20 │ -24234.2 5.6857 0.0691212 0.0481745 -6.76522e-5 0.0718787 ⋯
21 │ -24927.4 5.67965 0.066628 0.0441619 0.000997131 0.0939013 ⋯
22 │ -24044.7 5.68194 0.0675943 0.0364103 0.0108015 0.096463 ⋯
23 │ -24804.0 5.72333 0.0826845 0.0393307 0.00877465 0.0955252 ⋯
⋮ │ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋱confint(samp)DictTable with 2 columns and 38 rows:
par lower upper
────┬────────────────────────
β01 │ 5.65966 5.72791
β02 │ 0.0602683 0.0902347
β03 │ 0.0326438 0.0490006
β04 │ -0.00832038 0.0114628
β05 │ 0.0585181 0.124489
β06 │ 0.00932821 0.030229
β07 │ 0.00994937 0.0391542
β08 │ -0.0138358 0.00317468
β09 │ 0.00770406 0.0274789
β10 │ 0.00485596 0.0157058
β11 │ -0.00249685 0.0117935
β12 │ -0.0124823 0.00202088
β13 │ -0.00582681 0.0137215
β14 │ -0.00828443 0.00227533
β15 │ -0.00842329 0.00599236
β16 │ 0.00369609 0.0179879
ρ01 │ 0.380561 1.0
ρ02 │ -0.342485 0.999999
ρ03 │ -0.685044 0.682981
ρ04 │ 0.466487 0.989877
ρ05 │ 0.330399 0.883748
ρ06 │ -0.273379 0.932581
ρ07 │ -0.729693 -0.0549567
⋮ │ ⋮ ⋮We can also visualize the shortest coverage intervals for fixed effects with the ridgeplot() command:
ridgeplot(samp; show_intercept=false)
draw(
data(tbl) *
mapping(:σ => "Residual") *
density();
figure=(; resolution=(800, 400)),
)
The shortest coverage interval for the GM ranges from x to x ms and the associate variance component from .x to .x. To keep the plot range small we do not include their densities here.
rn = renamer([
"(Intercept)" => "GM",
"CTR: sod" => "spatial effect",
"CTR: dos" => "object effect",
"CTR: dod" => "attraction effect",
"(Intercept), CTR: sod" => "GM, spatial",
"(Intercept), CTR: dos" => "GM, object",
"CTR: sod, CTR: dos" => "spatial, object",
"(Intercept), CTR: dod" => "GM, attraction",
"CTR: sod, CTR: dod" => "spatial, attraction",
"CTR: dos, CTR: dod" => "object, attraction",
])
draw(
data(tbl) *
mapping(
[:β02, :β03, :β04] .=> "Experimental effect size [ms]";
color=dims(1) =>
renamer(["spatial effect", "object effect", "attraction effect"]) =>
"Experimental effects",
) *
density();
figure=(; resolution=(800, 350)),
)
The densitiies correspond nicely with the shortest coverage intervals.
draw(
data(tbl) *
mapping(
[:σ2, :σ3, :σ4] .=> "Standard deviations [ms]";
color=dims(1) =>
renamer(["spatial effect", "object effect", "attraction effect"]) =>
"Variance components",
) *
density();
figure=(; resolution=(800, 350)),
)
The VC are all very nicely defined.
draw(
data(tbl) *
mapping(
[:ρ01, :ρ02, :ρ03, :ρ04, :ρ05, :ρ06] .=> "Correlation";
color=dims(1) =>
renamer(["GM, spatial", "GM, object", "spatial, object",
"GM, attraction", "spatial, attraction", "object, attraction"]) =>
"Correlation parameters",
) *
density();
figure=(; resolution=(800, 350)),
)
Three CPs stand out positively, the correlation between GM and the spatial effect, GM and attraction effect, and the correlation between spatial and attraction effects. The second CP was positive, but not significant in the first study. The third CP replicates a CP that was judged questionable in script kwdyz11.jl.
The three remaining CPs are not well defined for log-transformed reaction times; they only fit noise and should be removed. It is also possible that fitting the complex experimental design (including target size and rectangle orientation) will lead to more acceptable estimates. The corresponding plot based on LMM m1_rt for raw reaction times still shows them with very wide distributions, but acceptable.